Ako nájsť množinu hodnôt funkcie z grafu. Funkcia: doména definície a rozsah hodnôt funkcií
GBOU Lyceum (Ekonomické) s. Isakly
Učiteľka matematiky Kuzaeva V.N.
2016
Referenčné materiály
Vzorový roztok Nájdite množinu funkčných hodnôt
Rozsah funkcií 
je
r - ľubovoľné číslo
Rozsah funkcií je
r
- ľubovoľné číslo
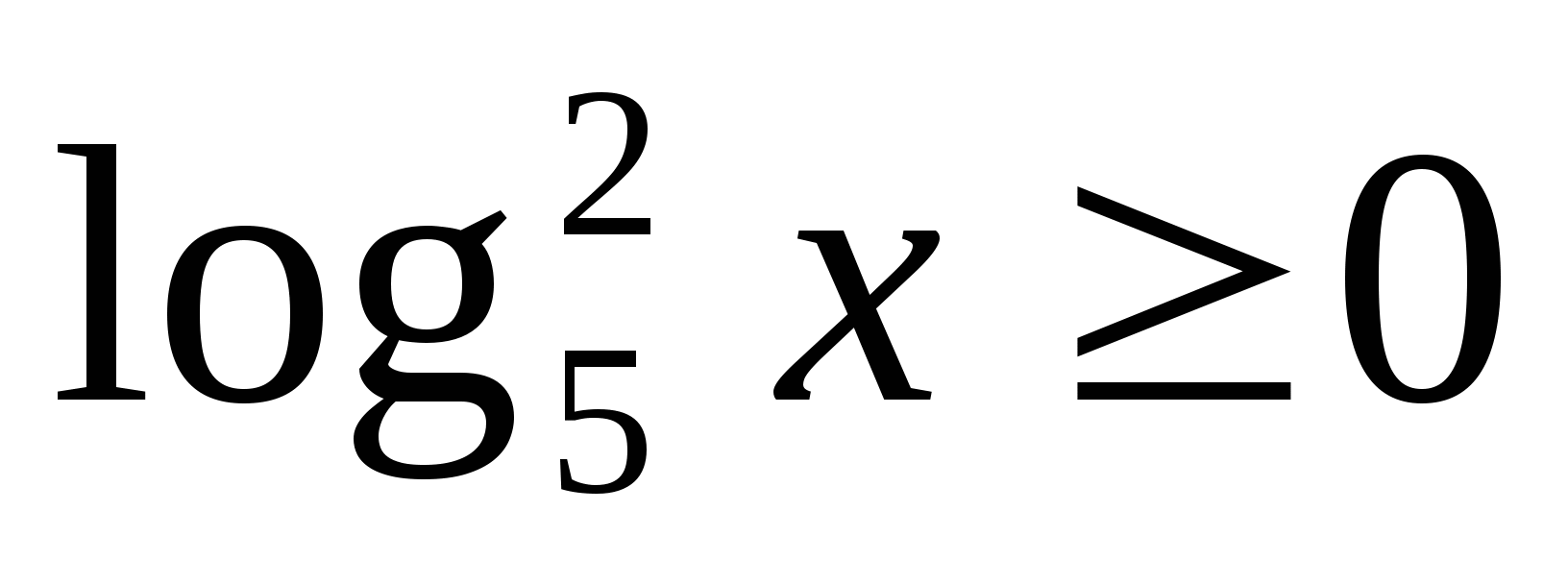
Viac významov
r - ľubovoľné číslo
Najvyššia hodnota
Najnižšia hodnota
doména X
- ľubovoľné číslo 
, Kde 
, Kde
Viac významov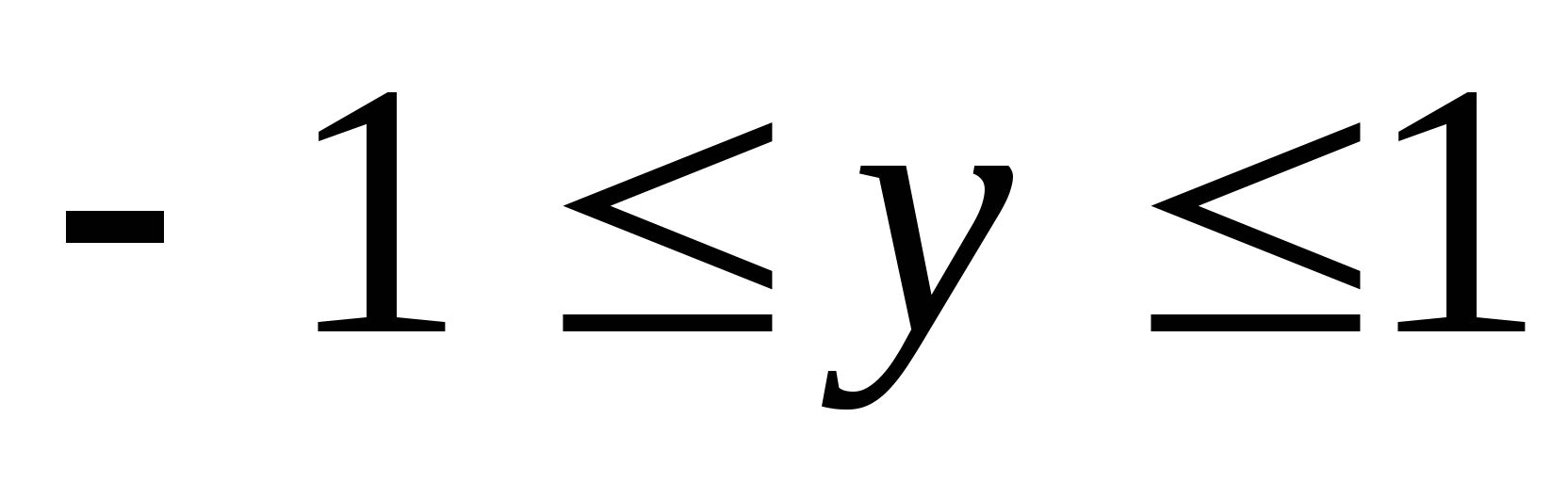 
r
- ľubovoľné číslor
- ľubovoľné číslo
Šablóny pre grafy niektorých goniometrických funkcií
Viacnásobné hodnoty goniometrických funkcií
možnosť 1
Y =hriech 3x+2.
1) (-5;5) 2) 3) 4) (1;5)
2. Nájdite rozsah funkcie y =tg x + 1.
1) 3) (-∞;∞) 4)
1) -6 2) 6 3) -4 4) -2
4. Zadajte najmenšie celé číslo v rozsahu funkcií
y = 12,7 + 5 hriech(3x-2).
1) -5 2) 8 3) 5 4) 17
5. Zadajte funkciu, ktorej množinou hodnôt je segment [-2;2].
1) y = cos 2x 2) y = hriech 2 X 3) r = cos 2 X +2
4) r = 2 hriech 4 X
6. Nájdite množinu funkčných hodnôtr =
tg 2
Xna segmente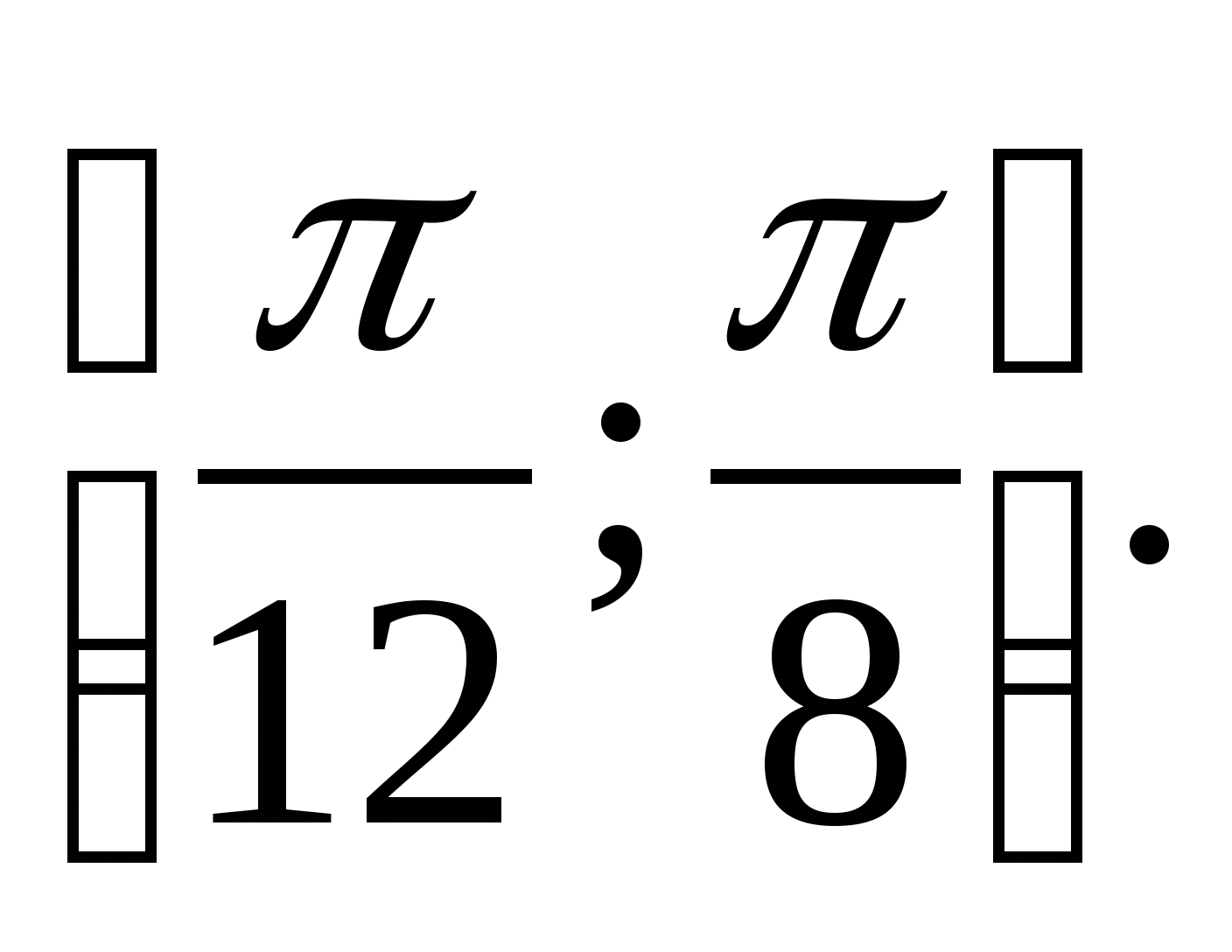 
7. Nájdite súčet všetkých celých čísel, ktoré sú zahrnuté v rozsahu funkcier = 4 cos 2 X – 7.
1) -25 2) 25 3) -22 4) 0
Možnosť 2
r = 2 cos 5 X +3.
1) (2;3) 2) 3) (1;5) 4) .
2. Nájdite rozsah funkcie 
1) 3) (-∞;∞) 4) .
3. Zadajte najmenšie číslo v rozsahu funkcií
1) 4 2) -3 3) 1 4) -7
4. Zadajte najväčšie celé číslo v rozsahu funkcií
1) 2 2) 13 3) 12 4) -2
5. Zadajte funkciu, ktorej množinou hodnôt je segment [-5;5].
1) y = hriech 5x 2) y = 5 cos 5x 3) y = cos (-5x)
4) y = hriech 5x + 5
6. Nájdite množinu funkčných hodnôt 
na segmente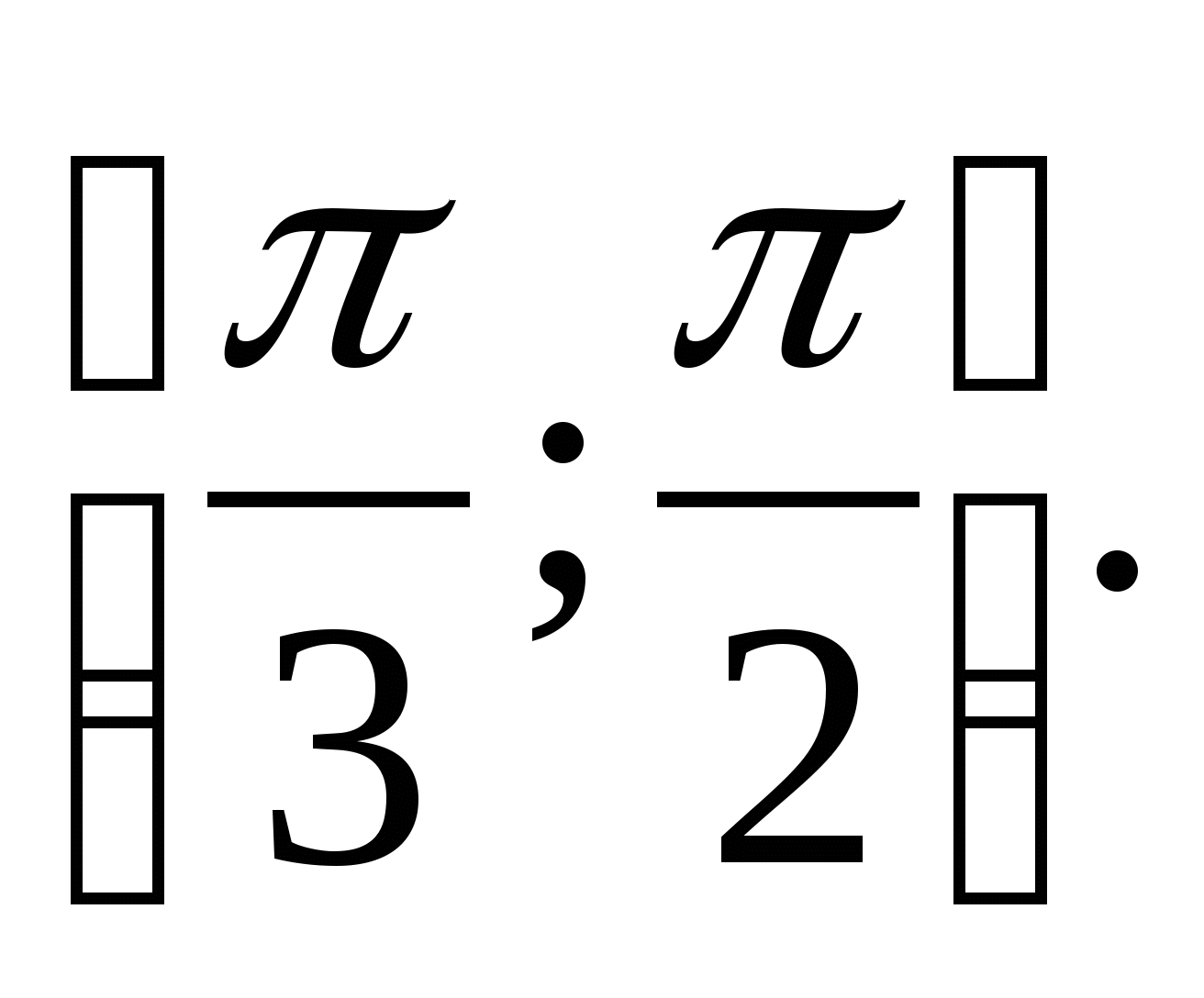 
7. Nájdite súčin všetkých celých čísel, ktoré sú zahrnuté v rozsahu hodnôt funkcie y = 5 – 3hriech 2 X.
1) 120 2) 14 3) -15 4) 0
Možnosť 3
1. Zadajte množinu funkčných hodnôtr =
hriech 3
X + 5.
1) (-4;6) 2) 3) [-1;5) 4) (0;6)
1) 2) (0;3) 3) (1;3) 4) [-1;3)
3. Zadajte najmenšie číslo z rozsahu hodnôt funkcie y = 5tg 2 X+2?
1) 5 2) 0 3) 7 4) 2
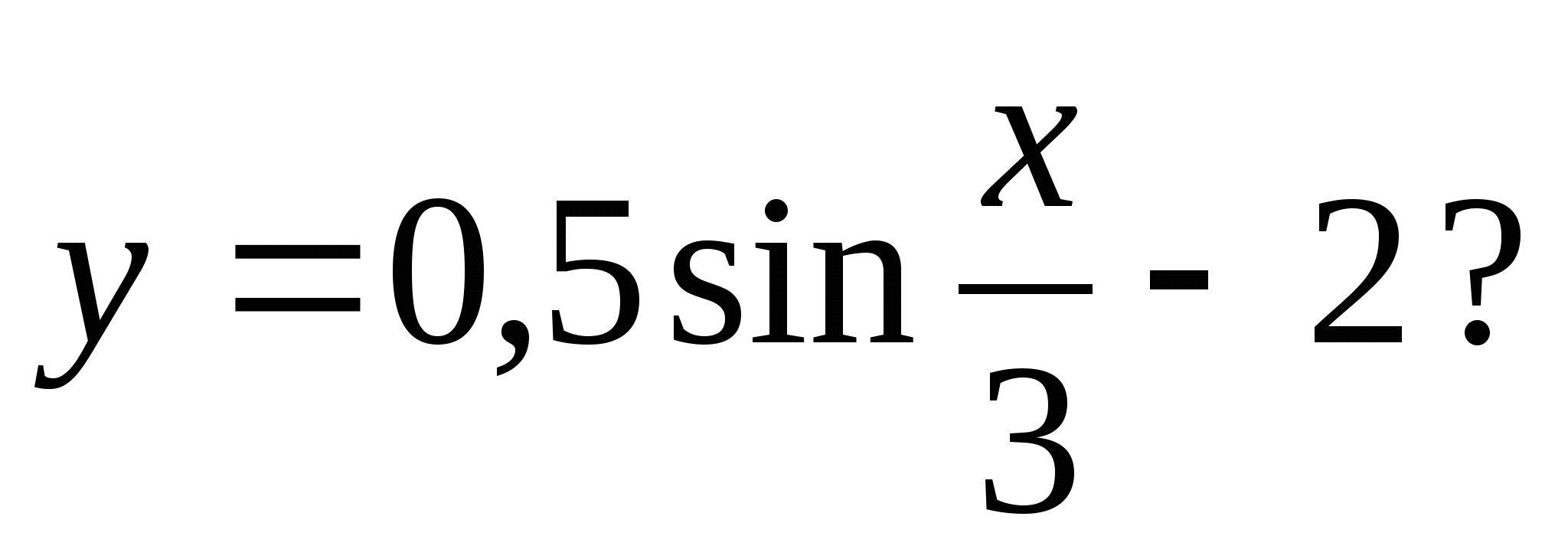
1) -1 2) -2,7 3) -2,3 4)-3
5. Zadajte funkciu, ktorej množinou hodnôt je segment
[-17;-13].
1) y = 5 sin x – 8 3) y = -cos x +15
2) y = 2 cos x – 15 4) y = 3 hriechy x +10
6. Zadajte najmenšie prirodzené číslo, ktoré nie je zahrnuté v množine funkčných hodnôt 
1) 2 2) 4 3) 15 4) 6
7. Koľko celých čísel patrí do množiny funkčných hodnôt
r = 2 cos 3 X +10?
1) 2 2) 3 3) 4 5) 5
Možnosť 4
1) 2) 4) (-7;-6)
2. Nájdite rozsah funkcie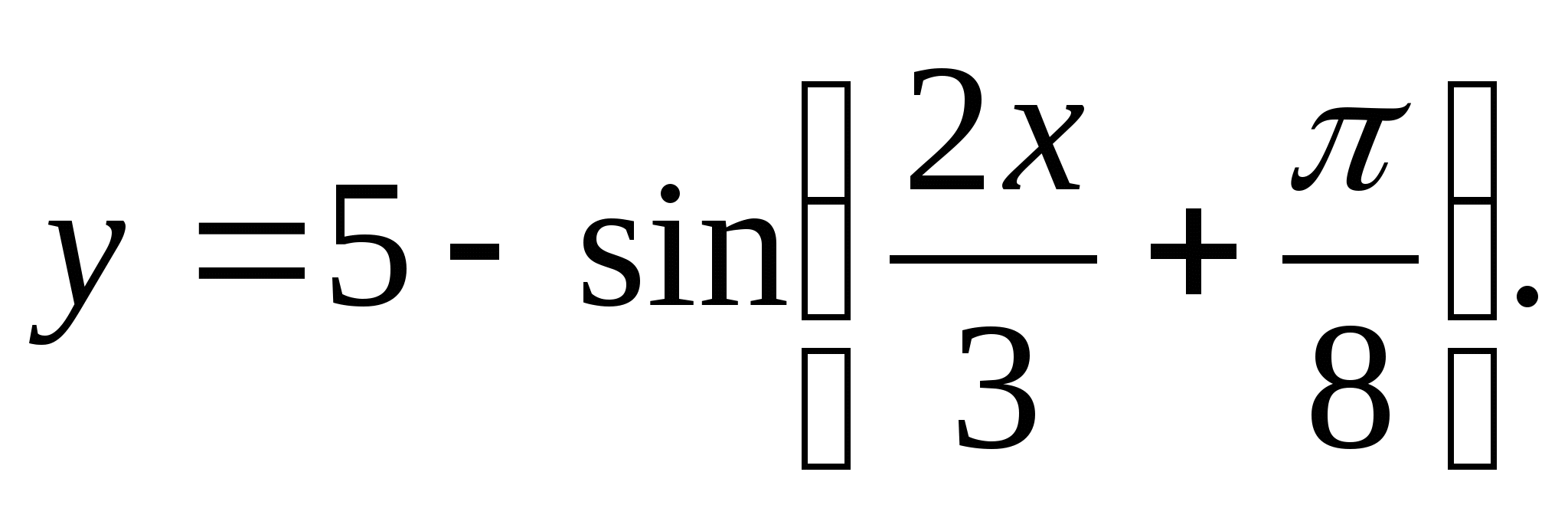 
1) (1;5) 2) 3) (4;6) 4) [-6;-4]
3. Uveďte najväčší počet z funkčného rozsahur = -3 ctg 2 X+7.
1) 10 2) 4 3) 7 4) -3
4. Ktoré z nasledujúcich čísel nie je zahrnuté v množine funkčných hodnôt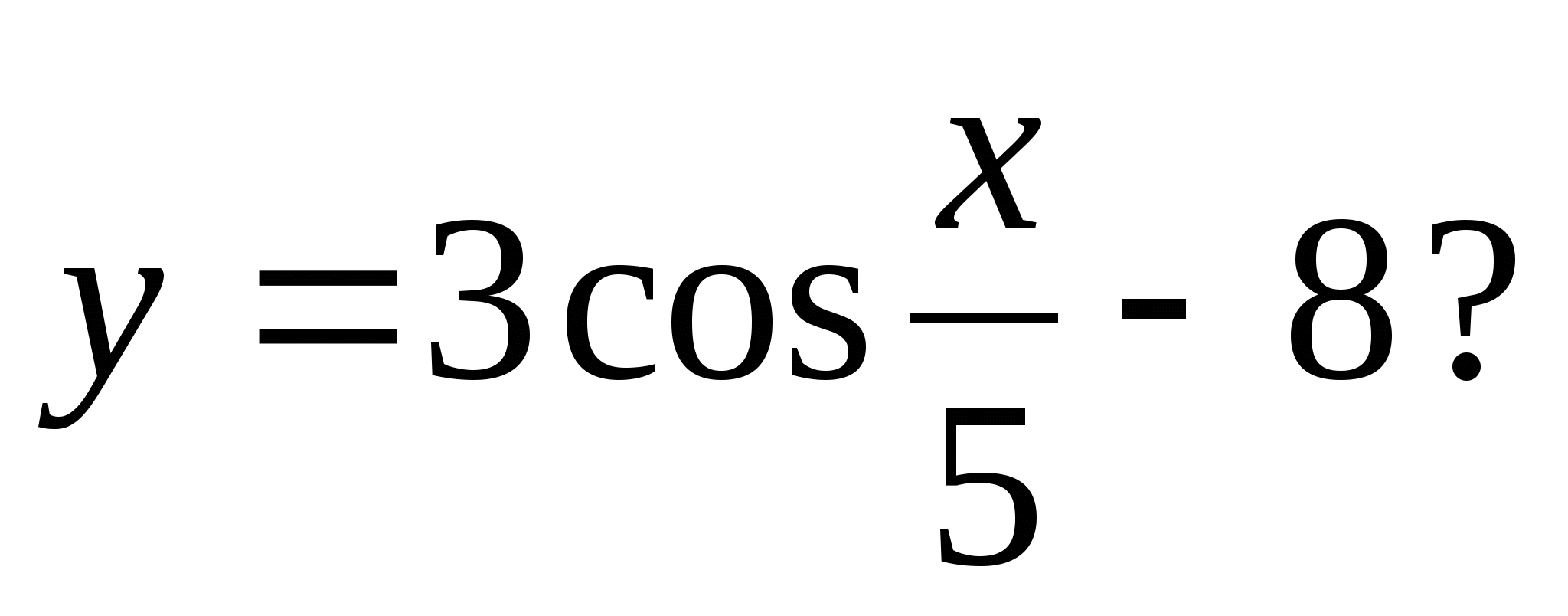 
1) -6 2) -5 3) -10 4) -7
5. Zadajte funkciu, ktorej množinou hodnôt je segment.
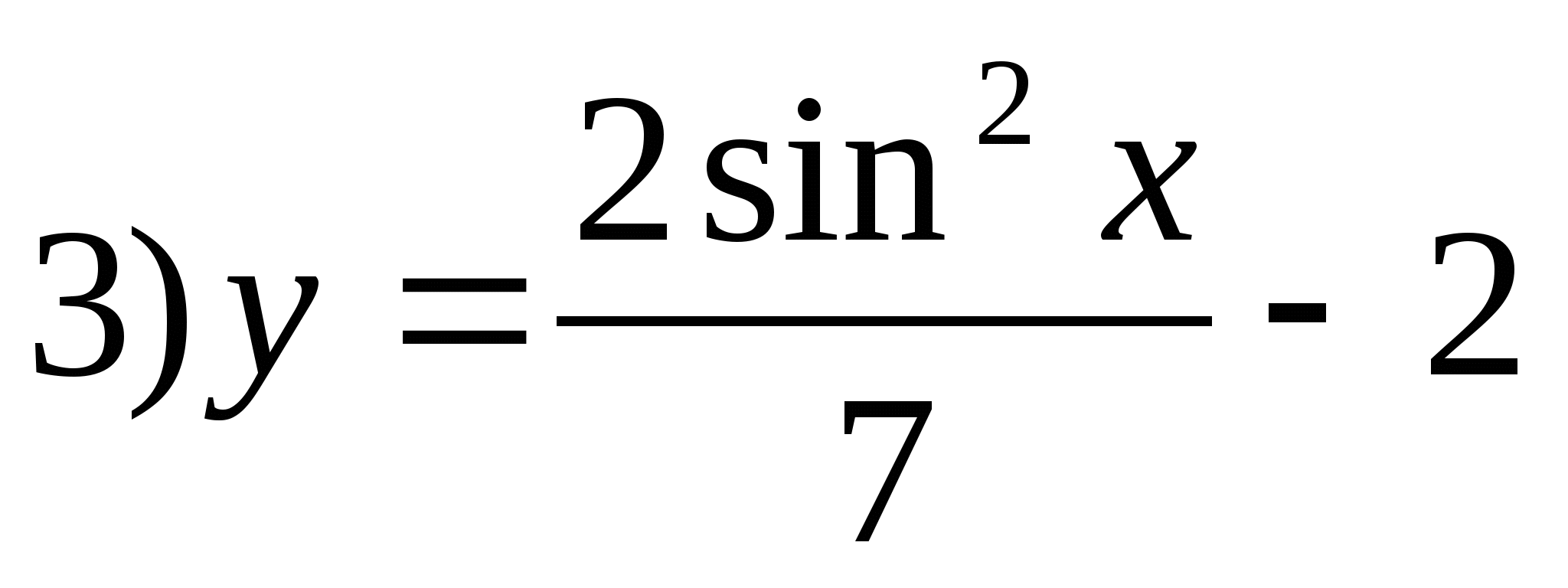
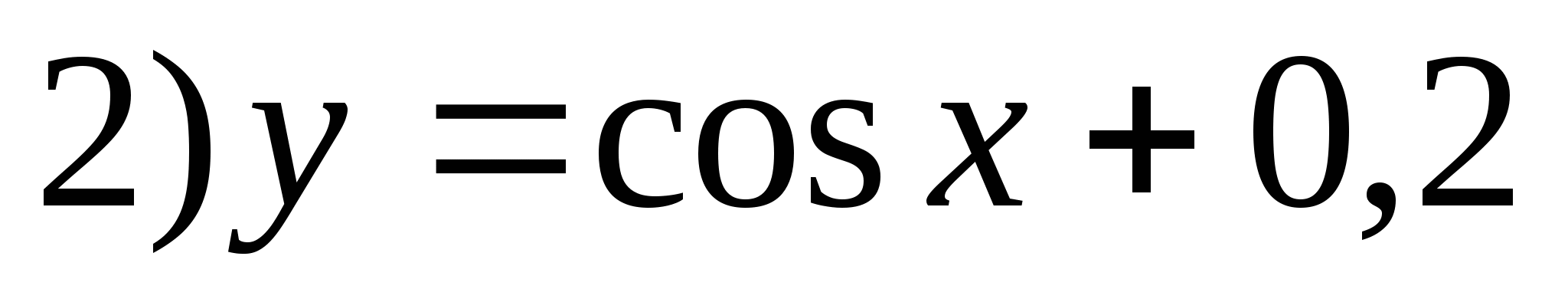
6. Zadajte najväčšie záporné celé číslo, ktoré nie je v rozsahu funkcie 
1) -1 2) -25 3) -6 4) -2
7. Koľko celých čísel patrí do množiny funkčných hodnôt 
1) 11 2) 3 3) 5 4) 4
Možnosť 5
1. Zadajte množinu hodnôt funkcie y = 2 -hriech 5 X.
1) (2;5) 2) 3) (1;3) 4) [-3;7]
2. Nájdite rozsah funkcie 
1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)
3. Zadajte najmenšie celé číslo v rozsahu funkcií
r = 3 + hriech 2 2 X.
1) 0 2) 1 3) 3 4) 4
4. Ktoré z nasledujúcich čísel je zahrnuté v množine funkčných hodnôt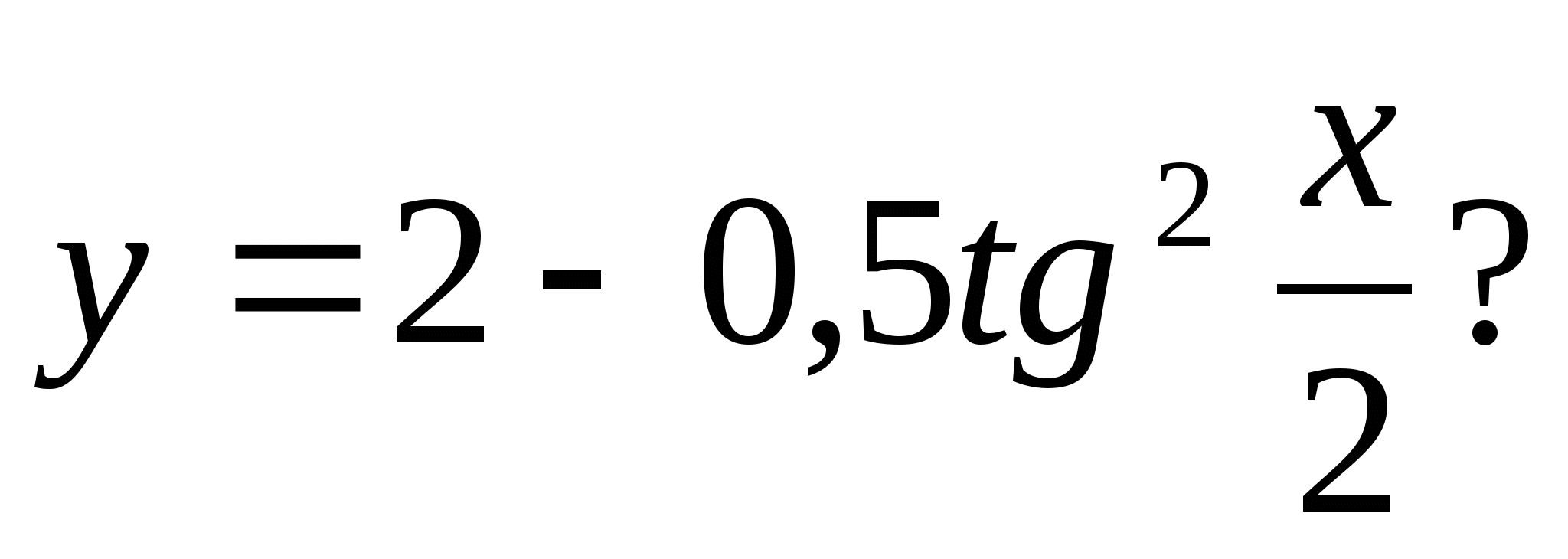 
1) 128 2) 10,5 3) 3 4) -235
5. Zadajte funkciu, ktorej množinou hodnôt je segment [-9;15].
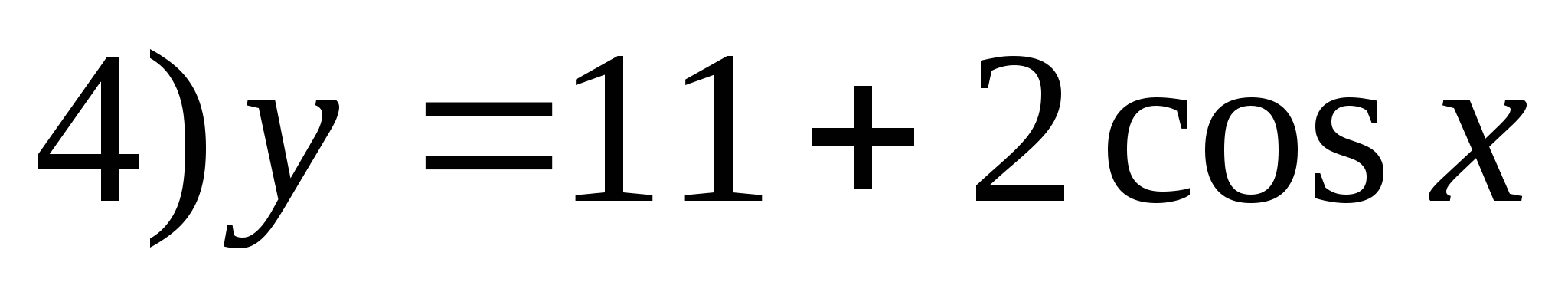
6. Nájdite súčet celých čísel zahrnutých v množine funkčných hodnôt 
1) 0 2) 7 3) 18 4) 22
7. Nájdite najvyššia hodnota funkcie 
na segmente 
1) 0,5 2) 1,5 3) 0 4) 2
Možnosť 6
1. Zadajte segment zodpovedajúci množine funkčných hodnôt 
1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]
2. Nájdite rozsah funkcie 
3. Zadajte najväčšie číslo v rozsahu funkcií 
1) 5 2) -6 3) -3 4) 4
4. Ktoré z nasledujúcich čísel je zahrnuté v množine funkčných hodnôt 
1) 5 2) 0 3) -3 4) 4
5. Zadajte funkciu, ktorej množinou hodnôt je segment.
1) pri = 15 – 7 cos 2x 3) y = 7 cos 2x + 3
2) r = 5 cos 4 X 4) r = - tg 2 X + 1
6. Nájdite súčin celých čísel zahrnutých v množine hodnôt
r = 3,8 – 1,4 hriech 3 X.
1) 17 2) 12 3) 0 4) 60
7. Nájdite množinu funkčných hodnôt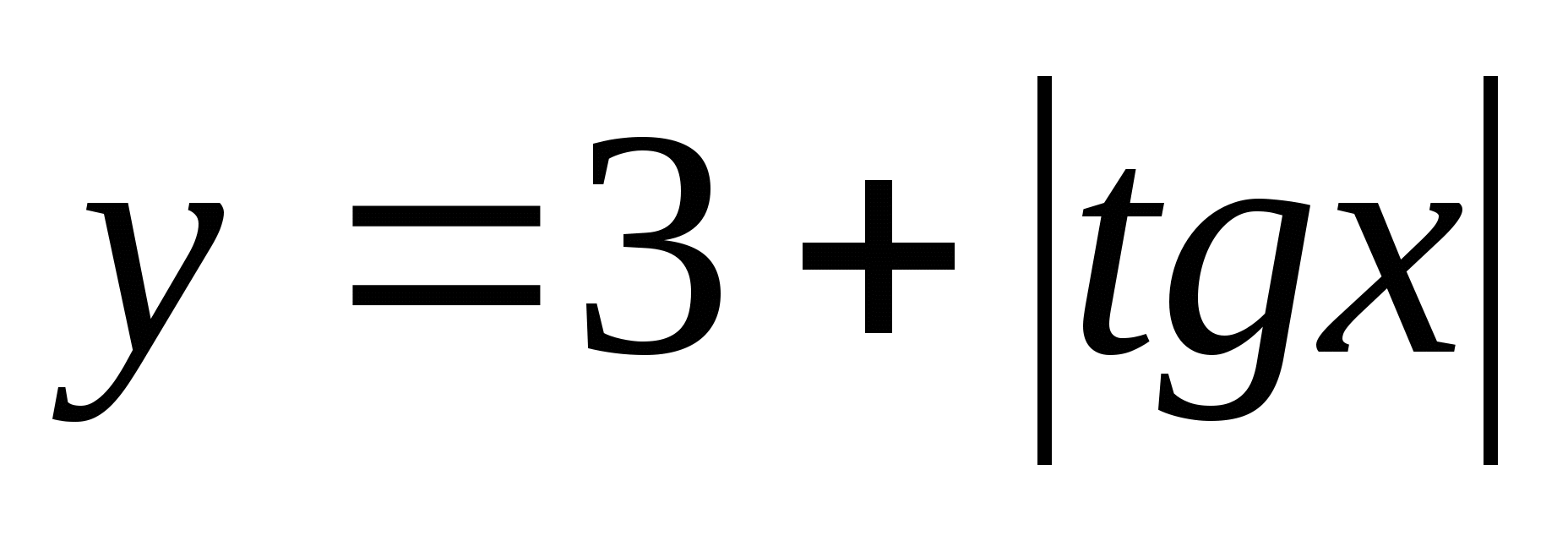 
medzi 
1) (3;4) 2) 3)
Možnosť 7
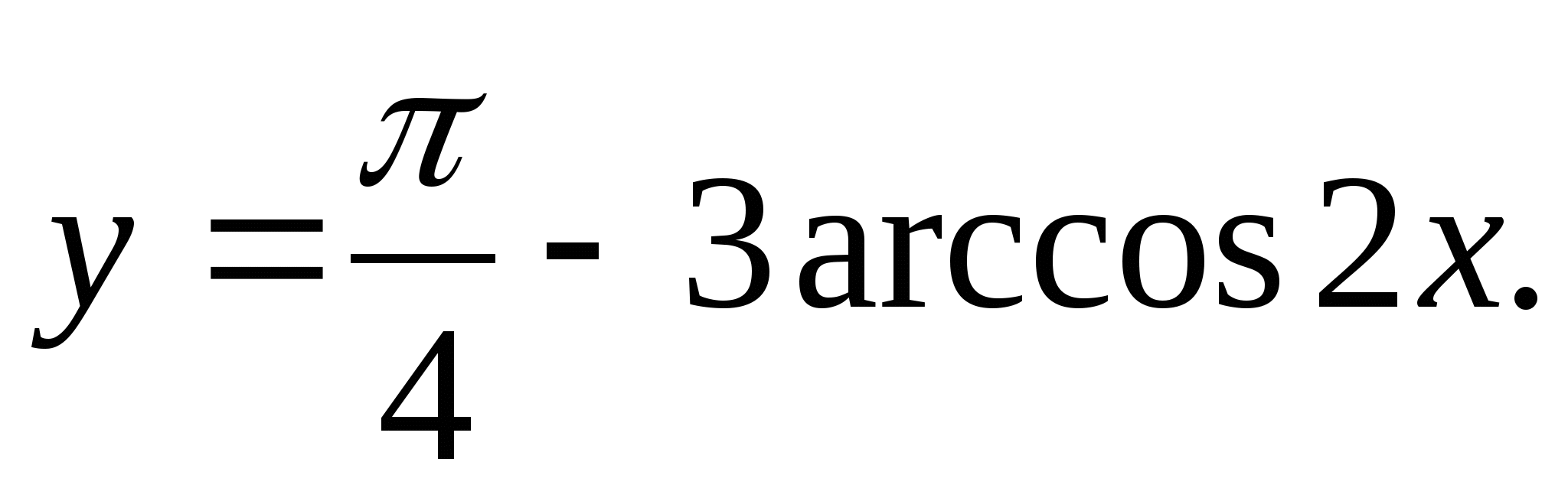
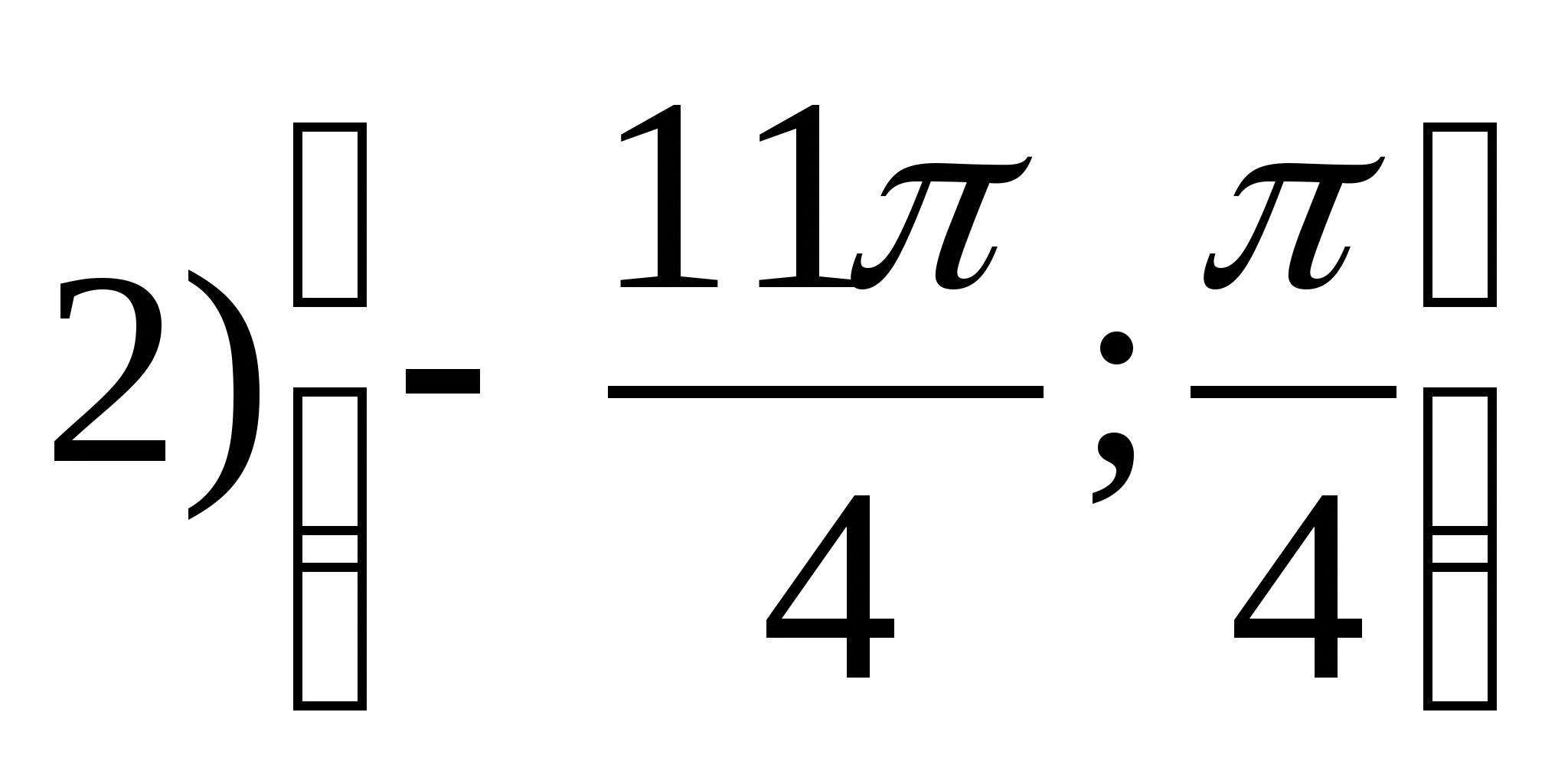
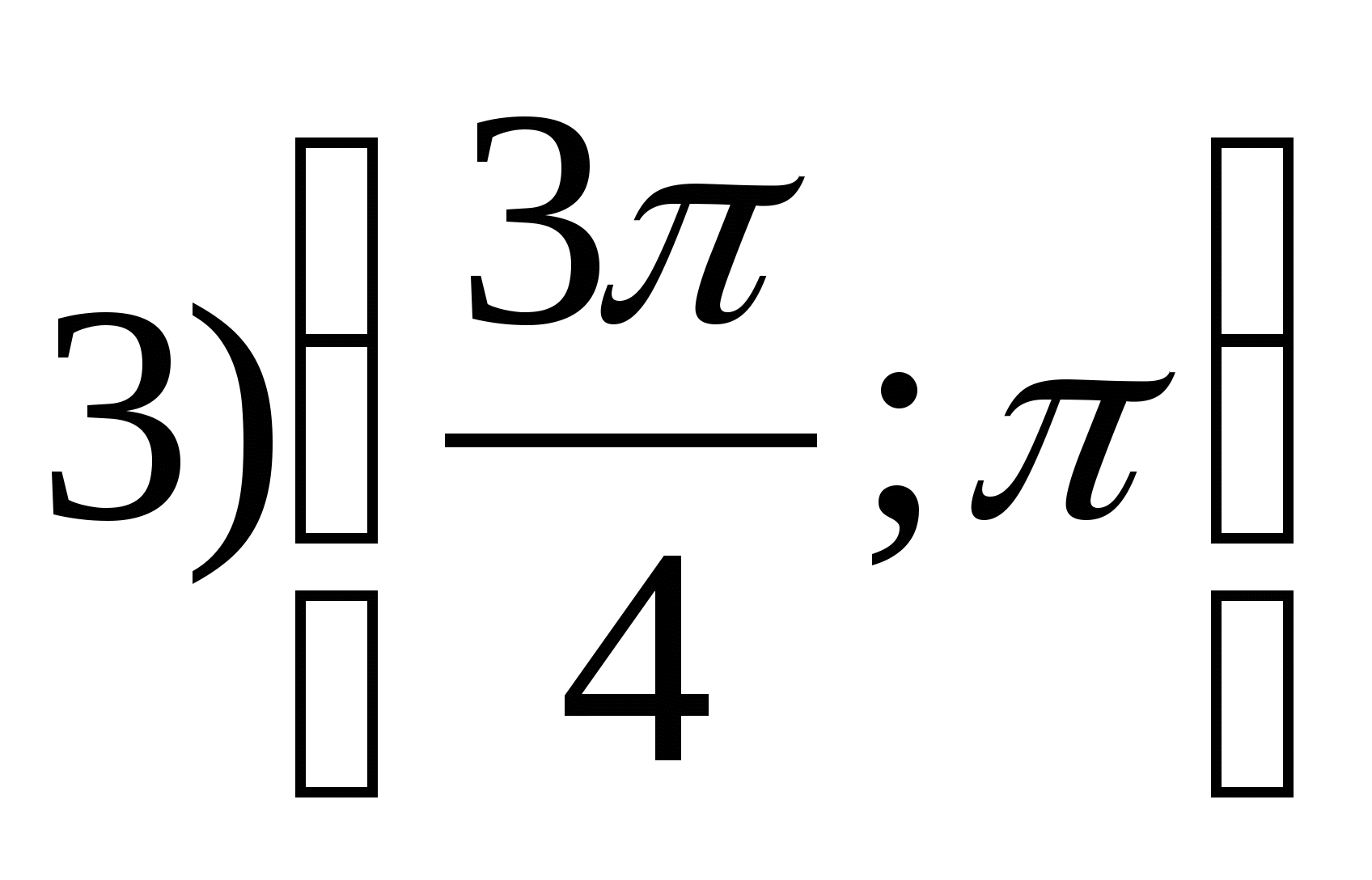
2. Nájdite najmenšiu celočíselnú hodnotu funkcie 
1) 2 2) 0 3) -3 4) -4
1) 0 2) 2 3) 4 4) 6
4. Pre aké hodnoty a je rovnicahriech(3 X-4)+5= a riešiteľný?
1) 2) 3) (4;6) 4) (-6;4]
hriech 2 2 X – 2.
1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]
medzi 
2) 0 3) 1
r = 4 hriech(X 4 ) -2?
1) 8 2) 9 3) 7 4) 10
Možnosť 8
1. Nájdite množinu funkčných hodnôtr = arctgX- 2π.
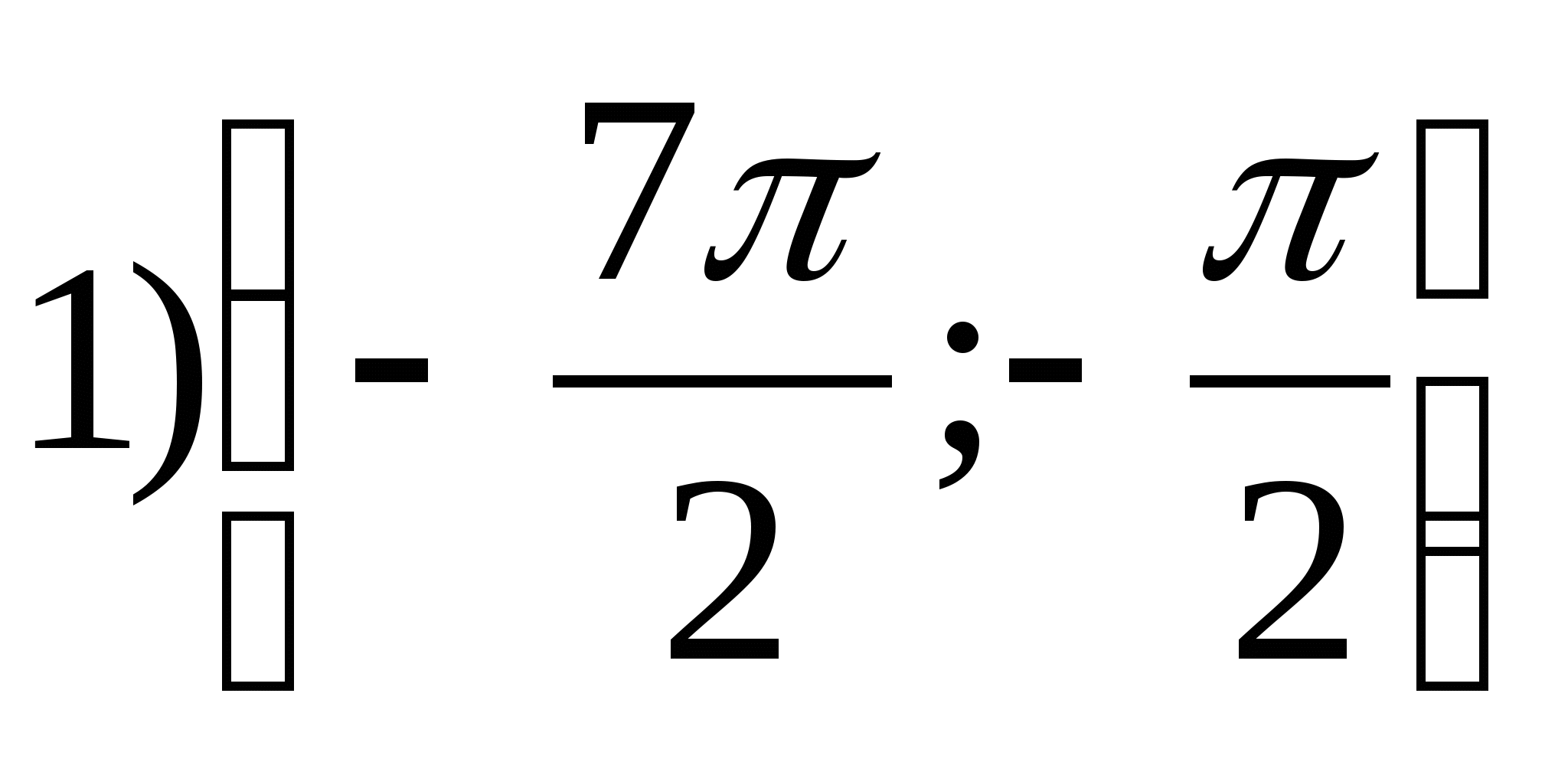
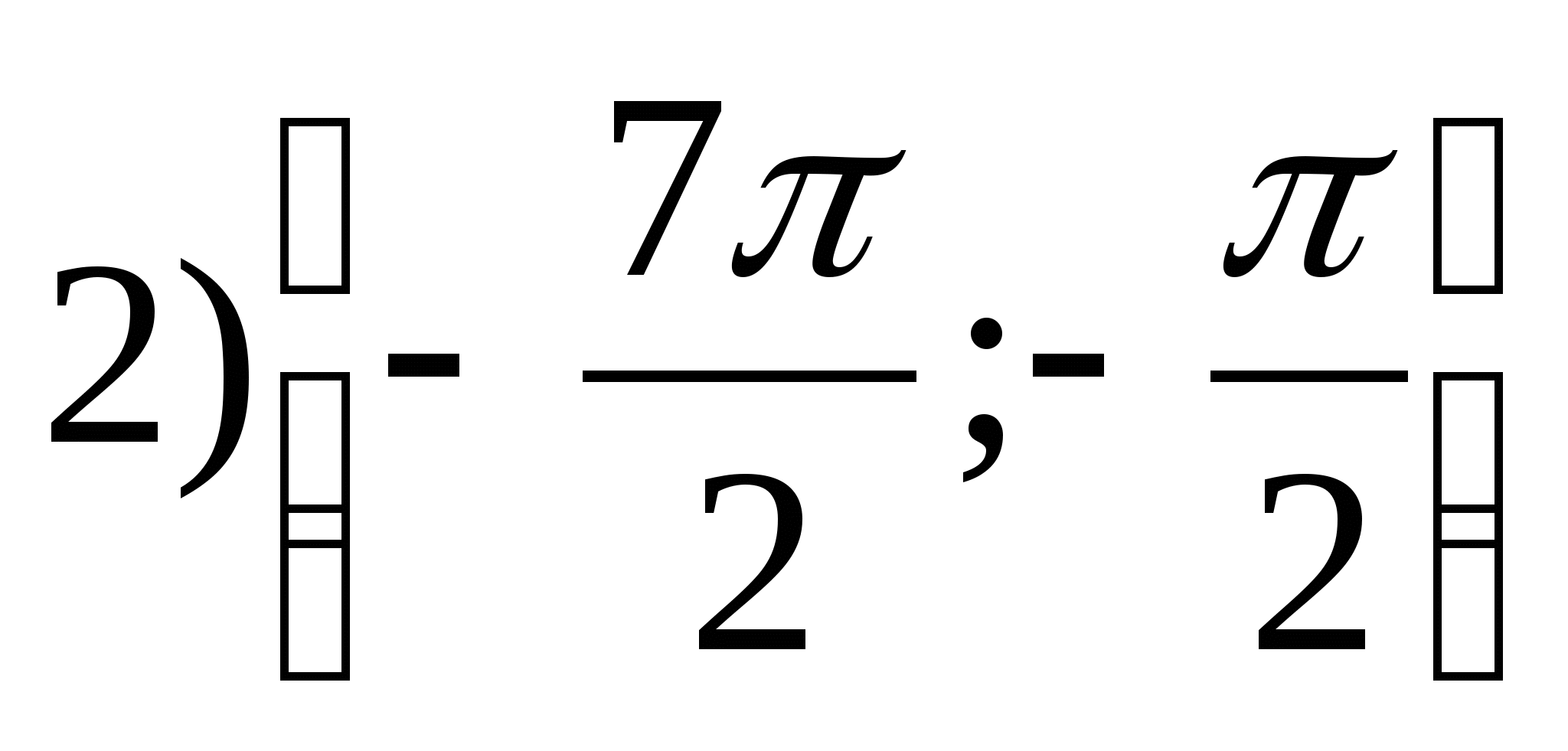
2. Nájdite najväčšiu hodnotu funkcie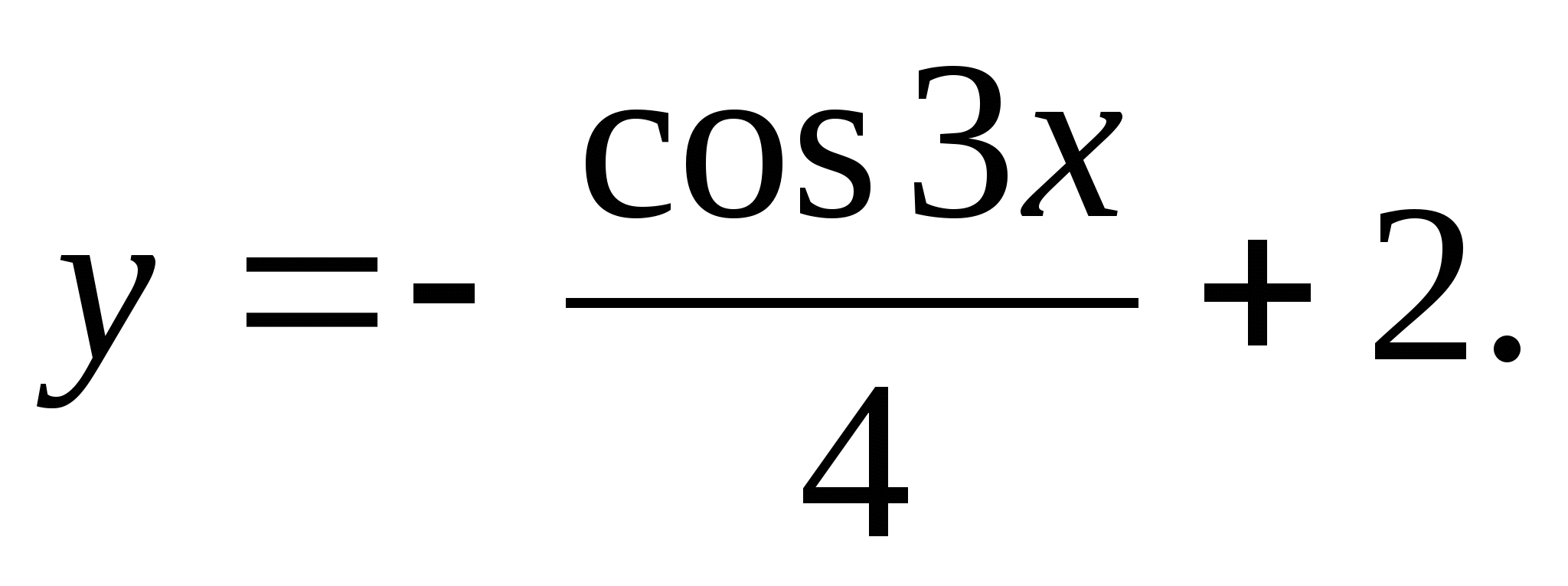 
1) 1,75 2) 0 3) 2,25 4) -1,75
3. Ktoré z nasledujúcich čísel by mohlo byť hodnotou funkcie 
1) -4 2) -2 3) 0 4) 2
4. Pri akých hodnotách p platí rovnica -2+cos(4 X-1)= p má korene?
1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)
5. Nájdite množinu funkčných hodnôtr = -2 tg 2 X + 1.
1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)
medzi 
.
1) 0 2) 1 3) -1 4) 3
7. Koľko celých čísel je vo funkčnom rozsahu
1) 4 2) 3 3) 5 4) 2
Možnosť 9
1. Nájdite rozsah funkcie 
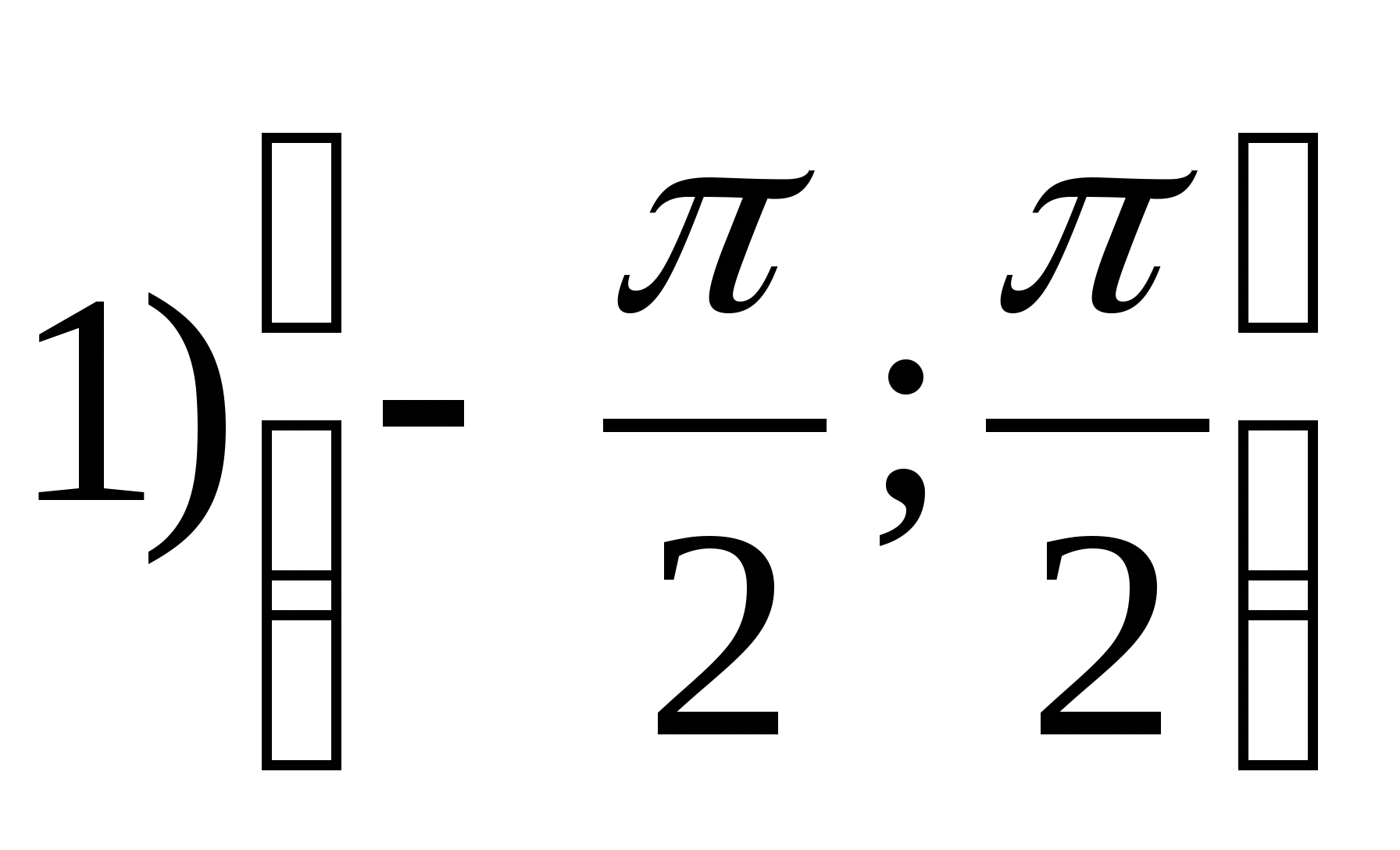
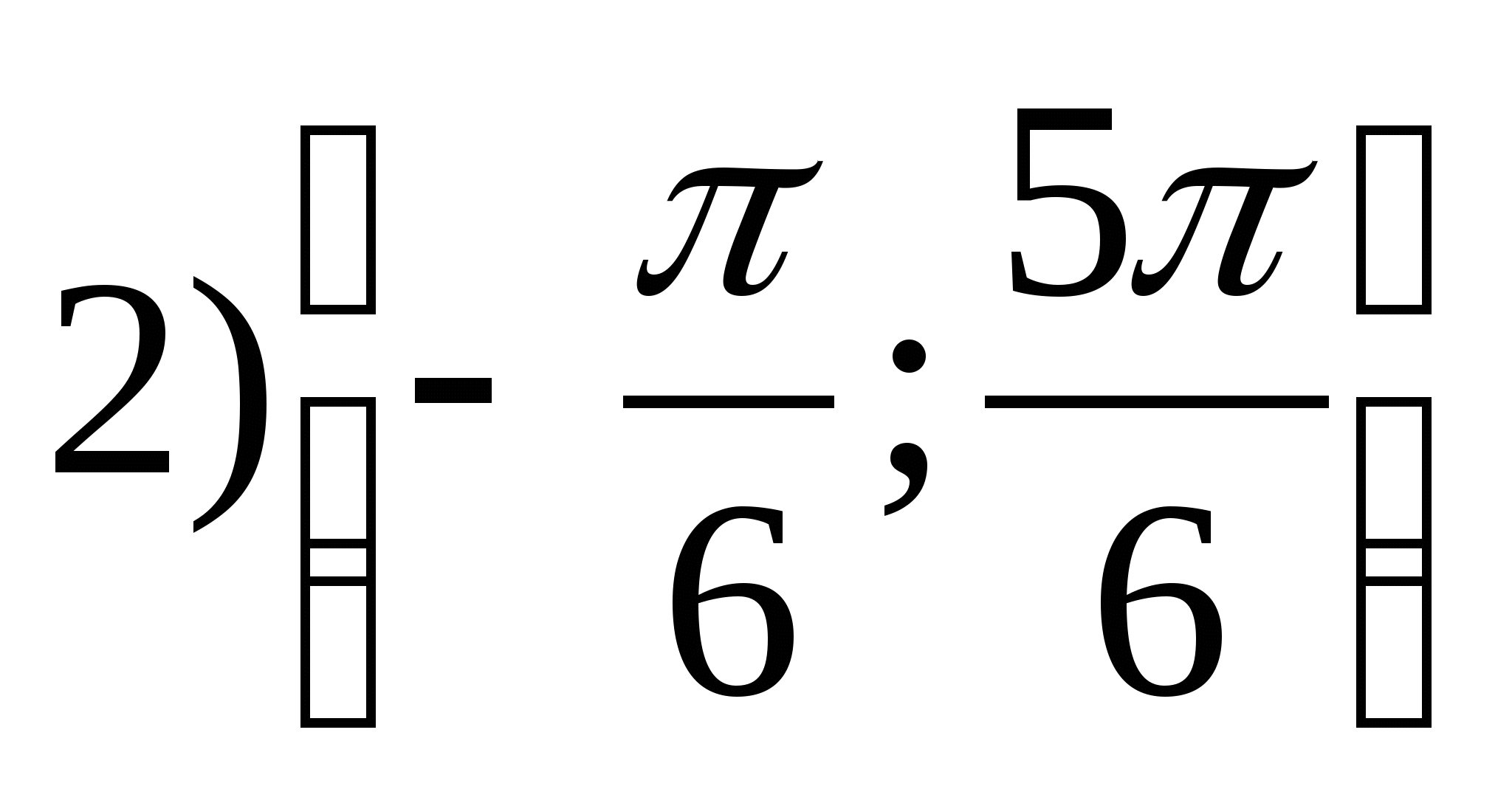
2. Nájdite najväčšiu celočíselnú hodnotu funkcie 
1) 4 2) 5 3) 6 4) 7
3. Ktoré z nasledujúcich čísel by mohlo byť hodnotou funkcie 
1) 0 2) 3 3) 6 4) 9
k rovnica - k + hriech(2 X-1) = 2 riešiteľné?
1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]
5. Nájdite množinu hodnôt funkcie y = -cos 2 3 X + 4.
1) 2) 3) 4)
6. Zadajte najmenšiu hodnotu funkcie medzi 
2) -1 3) 0 4) 1
7. Zistite, koľko celých čísel je zahrnutých v rozsahu hodnôt funkcie y = 12cos 3 X +5 hriech 3 X.
1) 13 2) 27 3) 26 4) 14
Možnosť 10
1. Nájdite rozsah funkcie 
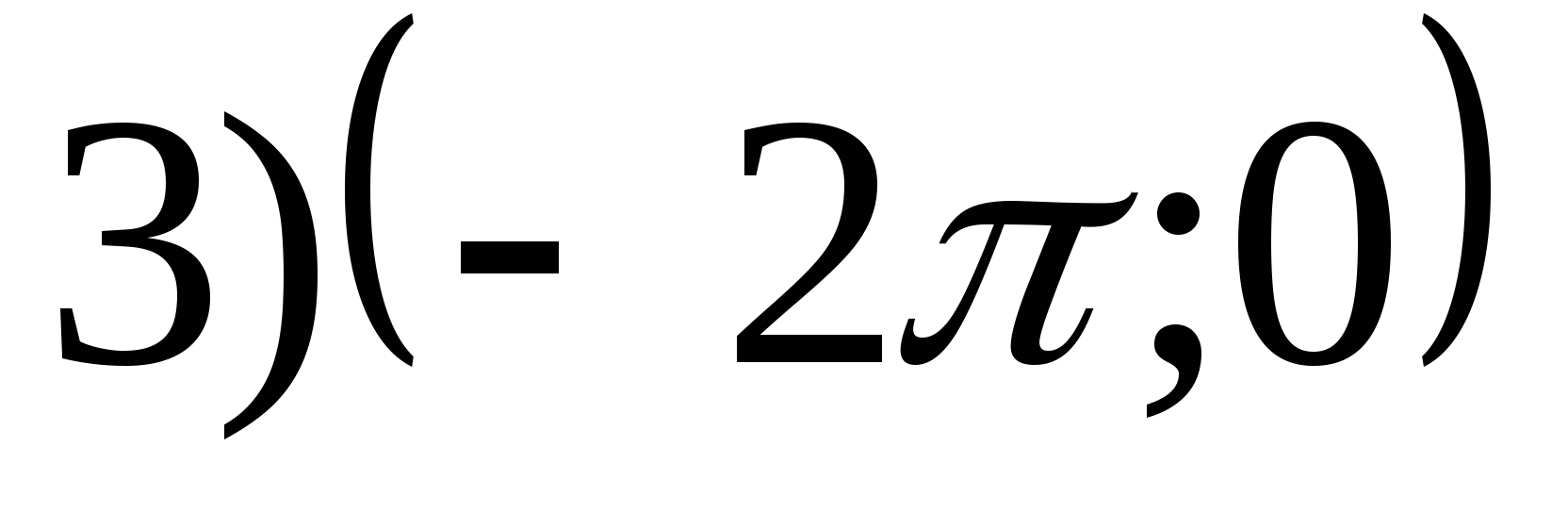
2. Nájdite najmenšiu hodnotu funkcie 
1) 3,5 2) 0 3) 2,5 4) -3,5
3. Ktoré z nasledujúcich čísel by mohlo byť hodnotou funkcie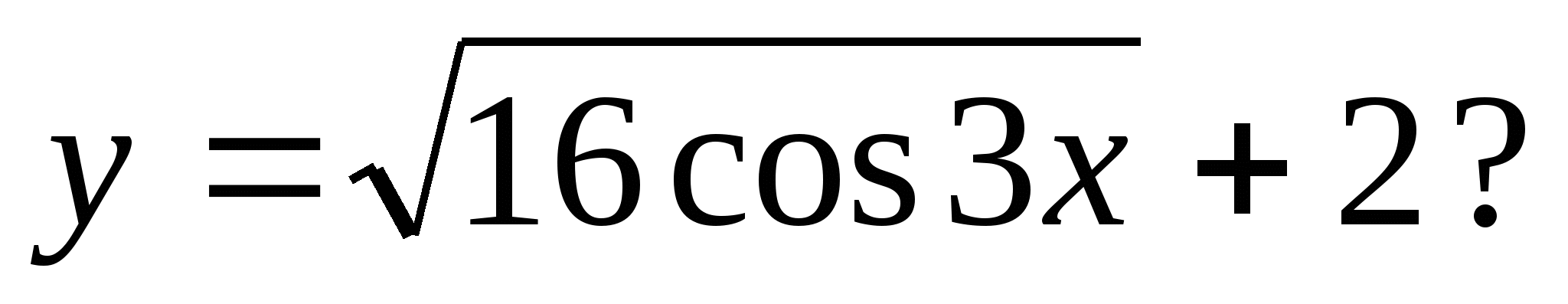 
1) -4 2) -1 3) 3 4) 7
4. Pri akých hodnotách parametrovm rovnica cos (3 X + 2)- m= 5 má korene?
1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]
5. Nájdite množinu hodnôt funkcie y = -2ctg 2 3 X + 7.
1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]
6. Zadajte najväčšiu hodnotu funkcie 
medzi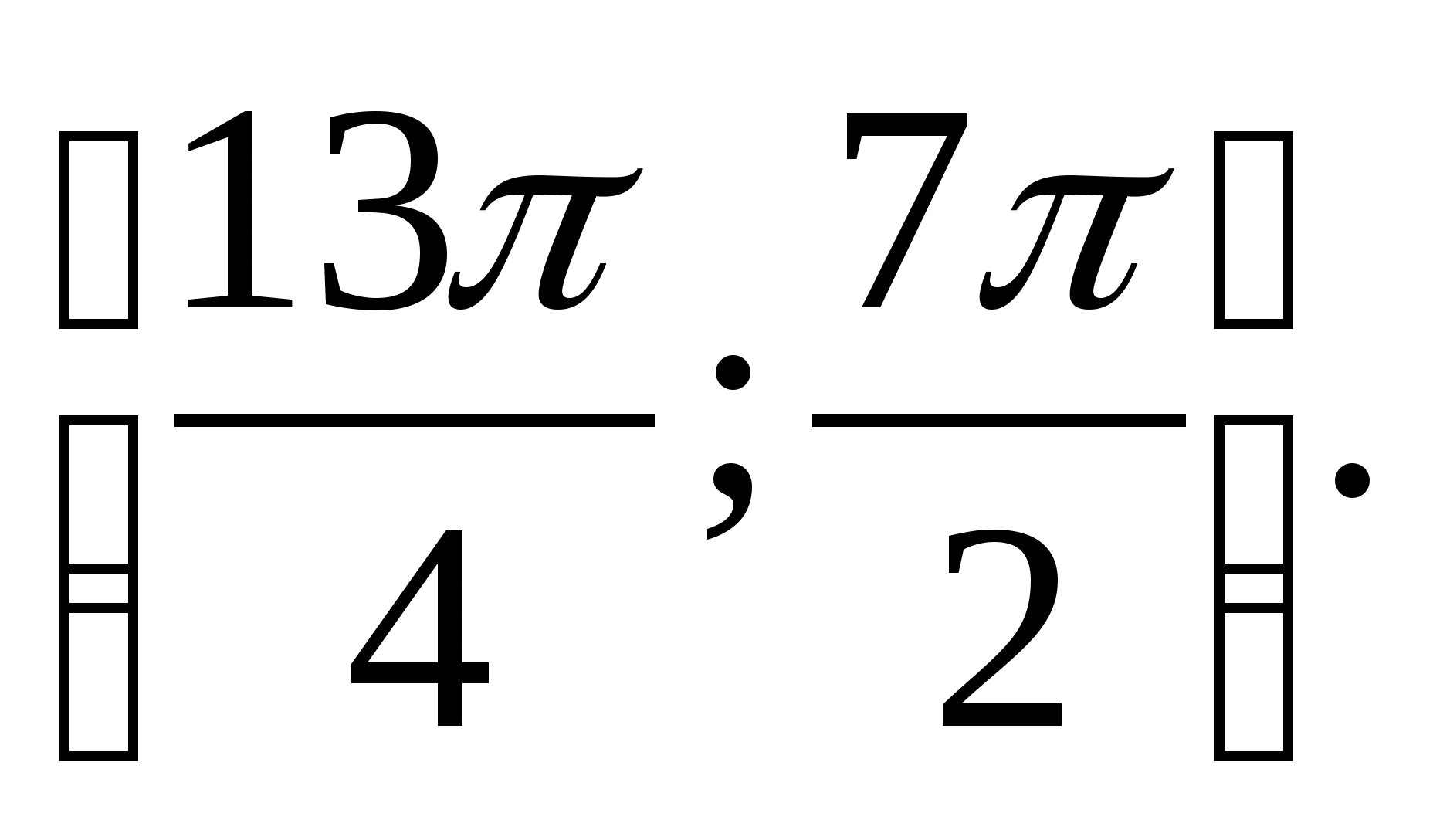 
2) 0 3) 2 4) 1
7. Zistite, koľko celých čísel je v rozsahu funkcie 
1) 30 2) 35 3) 17 4) 7
Viacnásobné hodnoty exponenciálnych a logaritmických funkcií
možnosť 1
1. Nájdite rozsah funkcie 
1) 4) (-∞;3)
2. Zadajte viacero funkčných hodnôt 
1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]
1) 0 2) 4 3) -3 4) -4
1) 15 2) 20 3) 43 4) 28
1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)
6. Zadajte najmenšiu celočíselnú hodnotu funkcie 
1) 1 2) -1 3) 0 4) -5
7. Zadajte funkciu, ktorej množinou hodnôt je interval (1;∞).
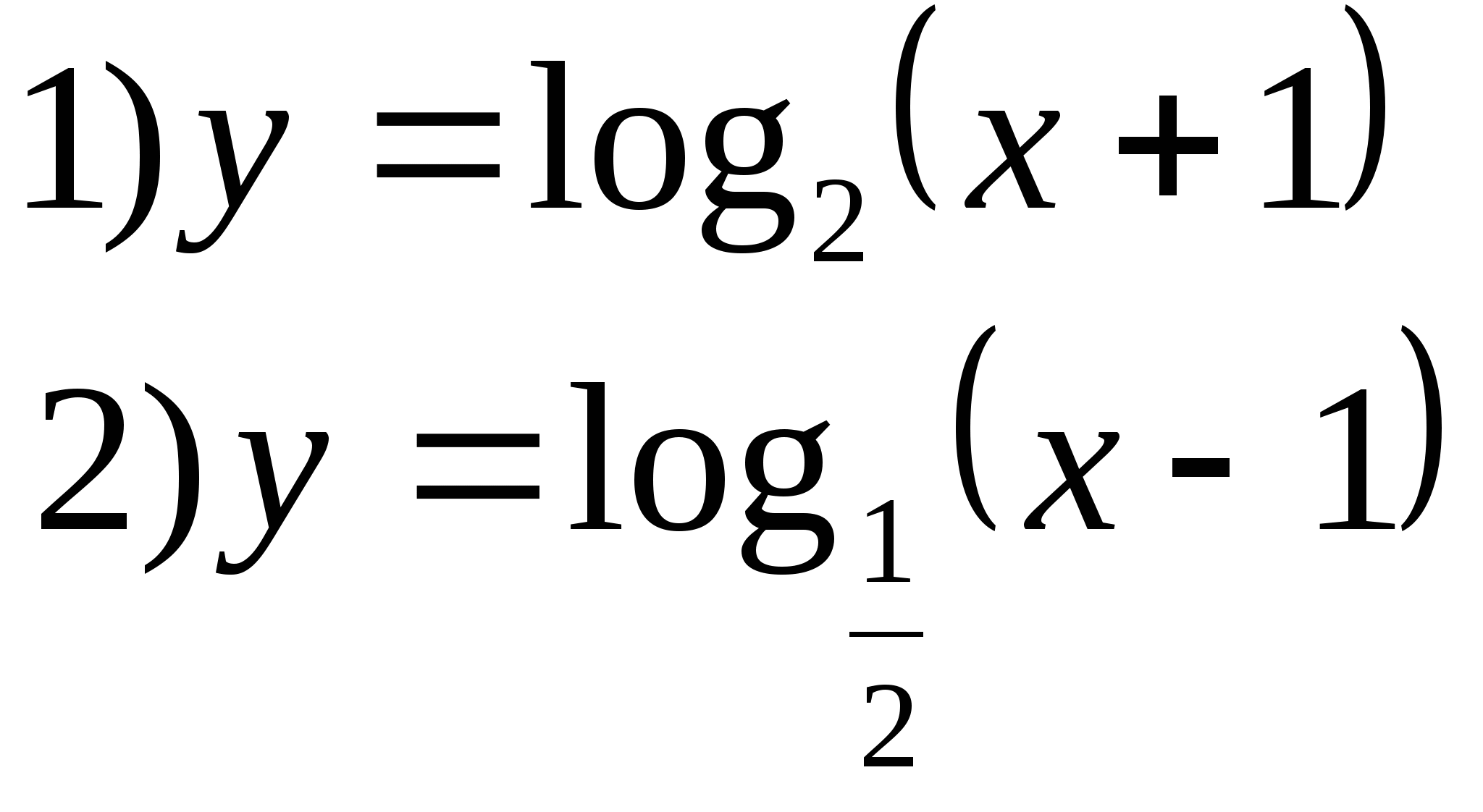
Možnosť 2
1. Zadajte množinu funkčných hodnôt 
1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)
2. Nájdite rozsah funkcie 
1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)
3. Zadajte najmenšiu celočíselnú hodnotu funkcie 
1) -12 2) -11 3) -10 4) -15
4. Zadajte číslo, ktoré nepatrí do množiny funkčných hodnôt 
1) -42 2) 3 3) 1 4) -20
5. Zadajte viacero funkčných hodnôt 
1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]
6. Zadajte najväčšiu celočíselnú hodnotu funkcie 
1) 10 2) 3 3) 9 4) 2
7. Zadajte funkciu, ktorej množinou hodnôt je interval
(-∞;13).
Možnosť 5
1. Zadajte najmenšiu celočíselnú hodnotu funkcie 
1) 0 2) -1 3) -2 4) -3
2. Ktoré z nasledujúcich čísel patrí do rozsahu funkcie 
1) -3 2) -4 3) 5 4) 0
1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)
6. Nájdite, na ktorom segmente je funkcia 
má najväčšiu hodnotu 2 a najmenšiu hodnotu -3.
1) 2) (-5;2) 3) 4) (-3;2)
medzi 
1) -1/2 2) 5 3) 2 4) 4
8. Nájdite súčet všetkých prirodzených čísel, ktoré nie sú zahrnuté v množine funkčných hodnôt 
1) 3 2) 6 3) 10 4) 8
Možnosť 6
1. Zadajte najväčšiu celočíselnú hodnotu funkcie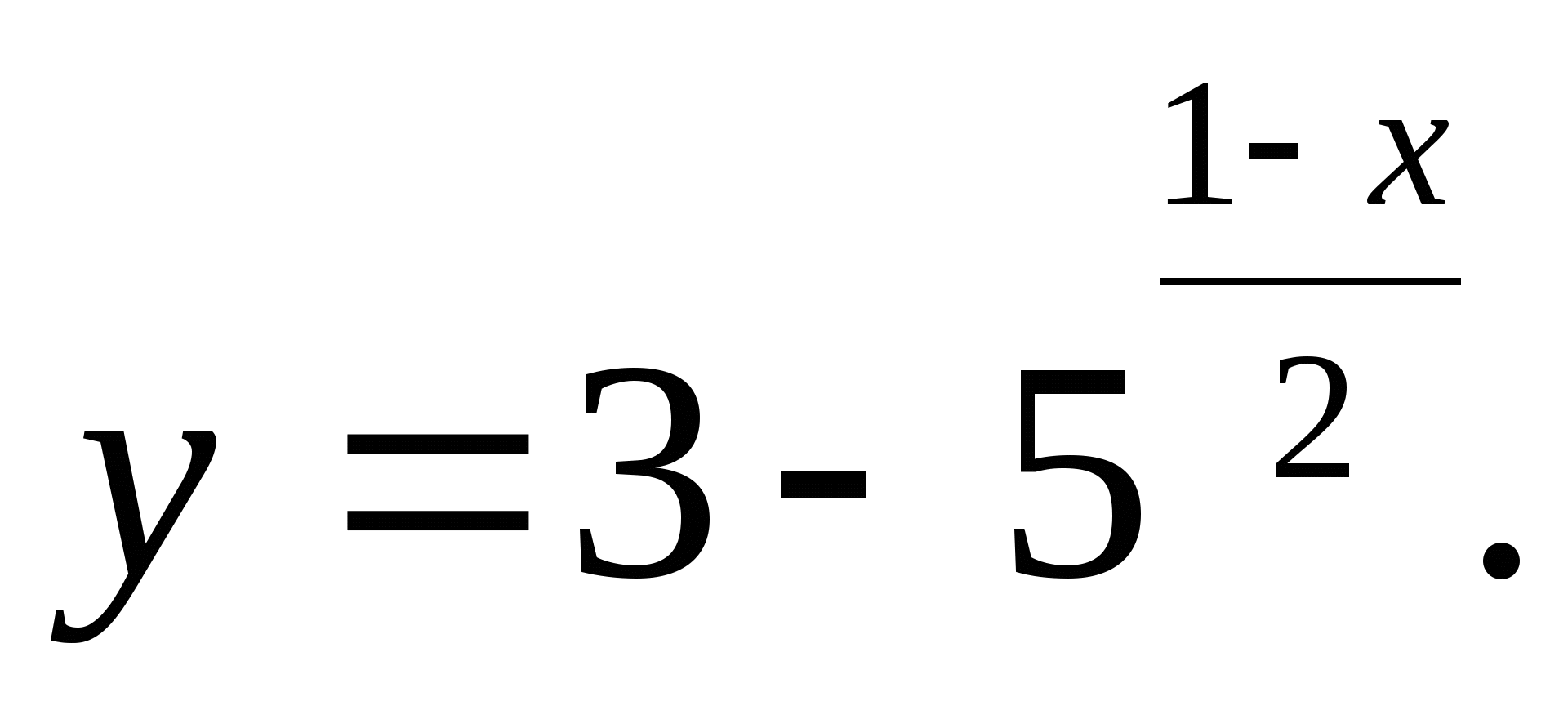 
1) 2 2) 4 3) 3 4) 5
2. Ktoré z nasledujúcich čísel nie je zahrnuté v rozsahu funkcie 
1) 35 2) 7, 28 3) 7, 85 4) 128
3. Zadajte viacero funkčných hodnôt 
1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)
4. Nájdite všetky body na operačnom zosilňovači, ktoré sú projekciou bodov na grafe funkcie 
1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)
6. Nájdite, na ktorom segmente je funkcia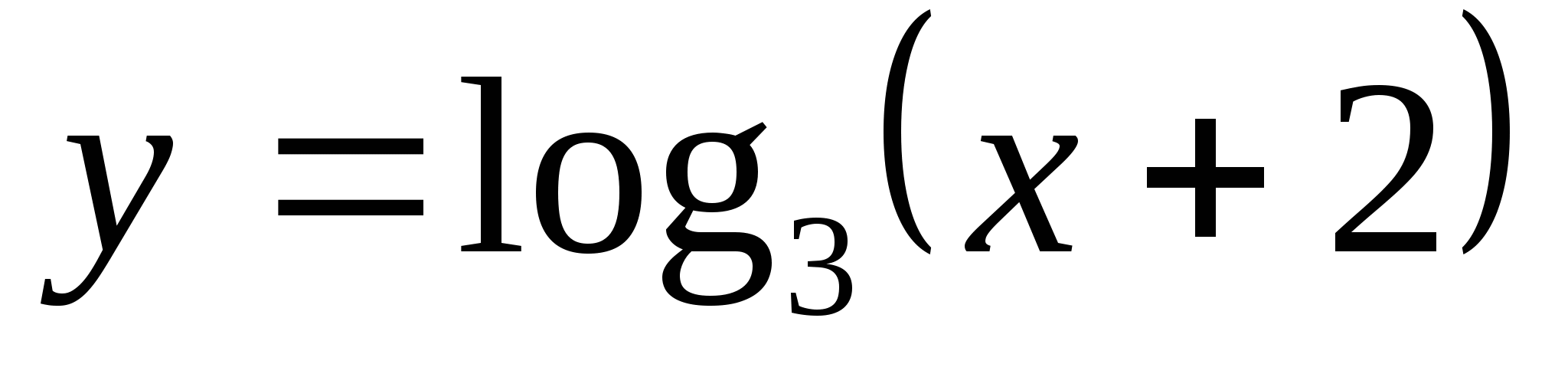 
má najmenšiu hodnotu -2 a najväčšiu hodnotu 4.
1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)
7. Zadajte najväčšiu hodnotu funkcie 
medzi
[-0,9; 0]. 2. Nájdite najmenšiu hodnotu funkcie na segmente.
4. Koľko celočíselných hodnôt má funkcia?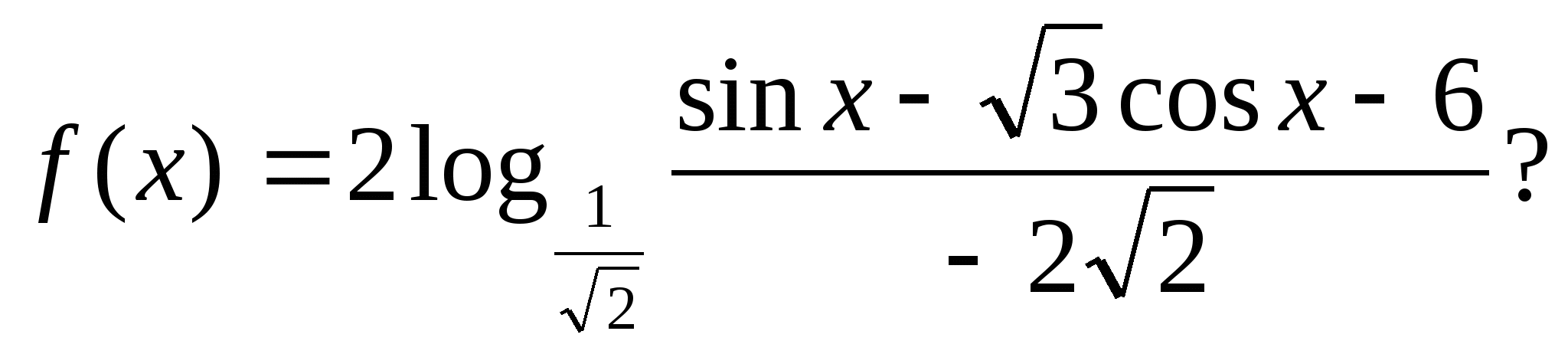 
Odpovede
Časť 1
Viacnásobné hodnoty exponenciálnych a logaritmických funkcií
Časť 2
Funkcia y=f(x) je taká závislosť premennej y od premennej x, kedy každej platnej hodnote premennej x zodpovedá jedna hodnota premennej y.
Doména definície funkcií D(f) je množina všetkých prijateľné hodnoty premenná x.
Rozsah funkcií E(f) je množina všetkých prípustných hodnôt premennej y.
Graf funkcie y=f(x) je množina bodov v rovine, ktorých súradnice spĺňajú danú funkčnú závislosť, teda body tvaru M (x; f(x)). Grafom funkcie je určitá priamka v rovine.
Ak b=0, funkcia bude mať tvar y=kx a bude volaná priama úmernosť.
D(f) : x \v R;\medzera E(f) : y \v R
Graf lineárnej funkcie je priamka.
Sklon k priamky y=kx+b sa vypočíta podľa tohto vzorca:
k= tan \alpha, kde \alpha je uhol sklonu priamky ku kladnému smeru osi Ox.
1) Funkcia monotónne rastie pre k > 0.
Napríklad: y=x+1
2) Funkcia monotónne klesá ako k< 0 .
Napríklad: y=-x+1
3) Ak k = 0, potom pri ľubovoľných hodnotách b dostaneme skupinu priamych čiar rovnobežných s osou Ox.
Napríklad: y=-1
Inverzná úmernosť
Inverzná úmernosť nazývaná funkcia formulára y=\frac (k)(x), kde k je nenulové reálne číslo
D(f) : x \in \left \( R/x \neq 0 \right \); \: E(f) : y \v \ľavo \(R/y \neq 0 \vpravo \).
Funkčný graf y=\frac (k)(x) je hyperbola.
1) Ak k > 0, potom sa graf funkcie bude nachádzať v prvej a tretej štvrtine súradnicovej roviny.
Napríklad: y=\frac(1)(x)
2) Ak k< 0 , то график функции будет располагаться во второй и четвертой координатной плоскости.
Napríklad: y=-\frac(1)(x)
Funkcia napájania
Funkcia napájania je funkciou tvaru y=x^n, kde n je nenulové reálne číslo
1) Ak n=2, potom y=x^2. D(f): x v R; \: E(f) : y \in; hlavná perióda funkcie T=2 \pi
Pojem funkcie a všetko, čo s tým súvisí, je tradične zložitý a nie úplne pochopený. Osobitným kameňom úrazu pri štúdiu funkcie a príprave na jednotnú štátnu skúšku je oblasť definície a rozsah hodnôt (zmeny) funkcie.
Študenti často nevidia rozdiel medzi doménou funkcie a doménou jej hodnôt.
A ak sa študentom podarí zvládnuť úlohy hľadania domény definície funkcie, potom im úlohy hľadania množiny hodnôt funkcie spôsobujú značné ťažkosti.
Účel tohto článku: zoznámiť sa s metódami hľadania funkčných hodnôt.
V dôsledku zváženia tejto témy sa študoval teoretický materiál, zvažovali sa metódy riešenia problémov hľadania množín funkčných hodnôt, didaktický materiál Pre samostatná prácaštudentov.
Tento článok môže učiteľ využiť pri príprave študentov na záverečné a prijímacie skúšky, pri štúdiu témy „Oblasť funkcie“ na výberových hodinách z matematiky.
I. Určenie rozsahu hodnôt funkcie.
Oblasť (množina) hodnôt E(y) funkcie y = f(x) je množina takých čísel y 0, z ktorých pre každé existuje číslo x 0 také, že: f(x 0) = y 0.
Pripomeňme si rozsahy hodnôt hlavných elementárnych funkcií.
Pozrime sa na tabuľku.
| Funkcia | Viac významov |
| y = kx+ b | E(y) = (-∞;+∞) |
| y = x2n | E(y) = |
| y = cos x | E(y) = [-1;1] |
| y = tan x | E(y) = (-∞;+∞) |
| y = ctg x | E(y) = (-∞;+∞) |
| y = arcsin x | E(y) = [-π/2; π/2] |
| y = arcos x | E(y) = |
| y = arktan x | E(y) = (-π/2 ; π/2) |
| y = arcctg x | E(y) = (0; π) |
Všimnite si tiež, že rozsah hodnôt ľubovoľného polynómu párneho stupňa je interval , kde n je najväčšia hodnota tohto polynómu.
II. Vlastnosti funkcií používaných pri hľadaní rozsahu funkcie
Ak chcete úspešne nájsť množinu hodnôt funkcie, musíte dobre poznať vlastnosti základných elementárnych funkcií, najmä ich definičné domény, rozsahy hodnôt a povahu monotónnosti. Uveďme si vlastnosti spojitých, monotónnych diferencovateľných funkcií, ktoré sa najčastejšie používajú pri hľadaní množiny funkčných hodnôt.
Vlastnosti 2 a 3 sa spravidla používajú spolu s vlastnosťou elementárnej funkcie byť spojitá vo svojom definičnom obore. V tomto prípade sa najjednoduchšie a najvýstižnejšie riešenie problému nájdenia množiny hodnôt funkcie dosiahne na základe vlastnosti 1, ak je možné jednoduchými metódami určiť monotónnosť funkcie. Riešenie problému je ešte jednoduchšie, ak je funkcia navyše párna alebo nepárna, periodická atď. Pri riešení problémov s hľadaním množín hodnôt funkcie by sme teda mali podľa potreby skontrolovať a použiť nasledujúce vlastnosti funkcie:
- kontinuita;
- monotónna;
- diferencovateľnosť;
- párne, nepárne, periodicita atď.
Jednoduché úlohy na nájdenie množiny hodnôt funkcie sú väčšinou orientované:
a) použiť najjednoduchšie odhady a obmedzenia: (2 x >0, -1≤sinx?1, 0≤cos 2 x?1 atď.);
b) na izoláciu celého štvorca: x 2 – 4x + 7 = (x – 2) 2 + 3;
c) transformovať goniometrické výrazy: 2sin 2 x – 3cos 2 x + 4 = 5sin 2 x +1;
d) pomocou monotónnosti funkcie x 1/3 + 2 x-1 sa zvýši o R.
III. Pozrime sa na spôsoby, ako nájsť rozsahy funkcií.
a) sekvenčné hľadanie hodnôt argumentov zložitých funkcií;
b) metóda odhadu;
c) využitie vlastností spojitosti a monotónnosti funkcie;
d) použitie derivátu;
e) použitie najväčšieho a najnižšie hodnoty funkcie;
f) grafická metóda;
g) metóda zadávania parametrov;
h) metóda inverznej funkcie.
Odhalme podstatu týchto metód na konkrétnych príkladoch.
Príklad 1: Nájdite rozsah E(y) funkcie y = log 0,5 (4 – 2 3 x – 9 x).
Vyriešme tento príklad postupným hľadaním hodnôt argumentov zložitých funkcií. Výberom dokonalého štvorca pod logaritmom transformujeme funkciu
y = log 0,5 (5 – (1 + 2 3 x – 3 2x)) = log 0,5 (5 – (3 x + 1) 2)
A postupne nájdeme množiny hodnôt jeho zložitých argumentov:
E(3 x) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2) = (-∞;4)
Označme t= 5 – (3 x +1) 2, kde -∞≤ t≤4. Problém sa teda redukuje na nájdenie množiny hodnôt funkcie y = log 0,5 t na lúči (-∞;4) . Keďže funkcia y = log 0,5 t je definovaná len pre, jej množina hodnôt na lúči (-∞;4) sa zhoduje s množinou funkčných hodnôt na intervale (0;4), ktorý je priesečníkom lúča (-∞;4) s doménou definície (0;+∞) logaritmickej funkcie. Na intervale (0;4) je táto funkcia spojitá a klesajúca. O t> 0 má tendenciu k +∞ a kedy t = 4 nadobúda hodnotu -2, takže E(y) =(-2, +∞).
Príklad 2: Nájdite rozsah funkcie
y = cos7x + 5cosx
Vyriešme tento príklad pomocou metódy odhadu, ktorej podstatou je odhadnúť spojitú funkciu zdola a zhora a dokázať, že funkcia dosahuje dolnú a hornú hranicu odhadov. V tomto prípade je zhoda množiny funkčných hodnôt s intervalom od dolnej hranice odhadu po hornú určená kontinuitou funkcie a absenciou iných hodnôt.
Z nerovností -1≤cos7x?1, -5≤5cosx?5 dostaneme odhad -6≤y?6. Pri x = p a x = 0 funkcia nadobúda hodnoty -6 a 6, t.j. dosahuje dolnú a hornú hranicu odhadu. Ako lineárna kombinácia spojitých funkcií cos7x a cosx je funkcia y spojitá na celej číselnej osi, preto vlastnosťou spojitej funkcie nadobúda všetky hodnoty od -6 do 6 vrátane a iba ich, keďže kvôli nerovnostiam -6≤y?6 iné hodnoty sú pre ňu nemožné. teda E(y)= [-6;6].
Príklad 3: Nájdite rozsah E(f) funkcie f(x)= cos2x + 2cosx.
Pomocou vzorca dvojitého uhla kosínus transformujeme funkciu f(x)= 2cos 2 x + 2cosx – 1 a označte t=cosx. Potom f(x)= 2t 2 + 2t – 1. Keďže E(cosx) =
[-1;1], potom rozsah hodnôt funkcie f(x) sa zhoduje s množinou hodnôt funkcie g (t)= 2t 2 + 2t – 1 na segmente [-1;1], ktorý zistíme graficky. Po vynesení funkcie y = 2t 2 + 2t – 1 = 2(t + 0,5) 2 – 1,5 na interval [-1;1] zistíme E(f) = [-1,5; 3].
Poznámka: veľa problémov s parametrom sa redukuje na nájdenie množiny hodnôt funkcie, ktoré súvisia najmä s riešiteľnosťou a počtom riešení rovníc a nerovníc. Napríklad rovnica f(x)= a je riešiteľné vtedy a len vtedy
a E(f) Rovnako tak Eq. f(x)= a má aspoň jeden koreň umiestnený na nejakom intervale X, alebo nemá jediný koreň na tomto intervale vtedy a len vtedy, ak a patrí alebo nepatrí do množiny hodnôt funkcie f(x) na intervale X. Študované aj pomocou súboru funkčných hodnôt a nerovností f(x)≠ A, f(x)> a, atď. najmä f(x)≠ a pre všetky prípustné hodnoty x, ak a E(f)
Príklad 4. Pre aké hodnoty parametra a má rovnica (x + 5) 1/2 = a(x 2 + 4) jeden koreň na intervale [-4;-1].
Napíšme rovnicu v tvare (x + 5) 1/2 / (x 2 + 4) = a. Posledná rovnica má aspoň jeden koreň na intervale [-4;-1] vtedy a len vtedy, ak a patrí do množiny hodnôt funkcie f(x) =(x + 5) 1/2 / (x 2 + 4) na segmente [-4;-1]. Nájdite túto množinu pomocou vlastnosti spojitosti a monotónnosti funkcie.
Na intervale [-4;-1] je funkcia y = xІ + 4 spojitá, klesajúca a kladná, preto funkcia g(x) = 1/(x 2 + 4) je spojité a na tomto segmente sa zväčšuje, keďže pri delení kladnou funkciou sa charakter monotónnosti funkcie mení na opačný. Funkcia h(x) =(x + 5) 1/2 je spojitá a rastúca vo svojej oblasti definície D(h) =[-5;+∞) a najmä na segmente [-4;-1], kde je navyše kladný. Potom funkcia f(x)=g(x) h(x), ako súčin dvoch spojitých, rastúcich a kladných funkcií, je tiež spojitý a rastúci na segmente [-4;-1], preto jeho množinou hodnôt na [-4;-1] je segment [ f(-4); f(-1)] = . V dôsledku toho má rovnica riešenie na intervale [-4;-1] a jednoznačné (na základe vlastnosti spojitej monotónnej funkcie) pre 0,05 ≤ a ≤ 0,4
Komentujte. Riešiteľnosť rovnice f(x) = a v určitom intervale X je ekvivalentné príslušnosti k hodnotám parametra A súbor funkčných hodnôt f(x) na X. Následne množina hodnôt funkcie f(x) na intervale X sa zhoduje so súborom hodnôt parametrov A, pre ktoré platí rovnica f(x) = a má aspoň jeden koreň na intervale X. Najmä rozsah hodnôt E(f) funkcie f(x) zodpovedá množine hodnôt parametrov A, pre ktoré platí rovnica f(x) = a má aspoň jeden koreň.
Príklad 5: Nájdite rozsah E(f) funkcie
Vyriešme príklad zavedením parametra, podľa ktorého E(f) zodpovedá množine hodnôt parametrov A, pre ktoré platí rovnica
má aspoň jeden koreň.
Keď a = 2, rovnica je lineárna - 4x - 5 = 0 s nenulovým koeficientom pre neznáme x, preto má riešenie. Pre a≠2 je rovnica kvadratická, takže je riešiteľná vtedy a len vtedy, ak je jej diskriminant
Keďže bod a = 2 patrí do segmentu
potom požadovaný súbor hodnôt parametrov A, teda rozsah hodnôt E(f) bude celý segment.
Za priamy vývoj metódy zavedenia parametra pri hľadaní množiny funkčných hodnôt môžeme považovať metódu inverznej funkcie, na nájdenie ktorej je potrebné vyriešiť rovnicu pre x f(x)=y, pričom y považujeme za parameter. Ak má táto rovnica jedinečné riešenie x =g(y), potom rozsah hodnôt E(f) pôvodná funkcia f(x) sa zhoduje s doménou definície D(g) inverzná funkcia g(y). Ak rovnica f(x)=y má viacero riešení x = g 1 (y), x = g 2 (y) atď., teda E(f) sa rovná zjednoteniu domén funkcie g 1 (y), g 2 (y) atď.
Príklad 6: Nájdite rozsah E(y) funkcie y = 5 2/(1-3x).
Z rov.
nájdime inverznú funkciu x = log 3 ((log 5 y – 2)/(log 5 y)) a jej definičný obor D(x):
Pretože rovnica pre x má jedinečné riešenie
E(y) = D(x) = (0; 1) (25;+°).
Ak oblasť definície funkcie pozostáva z niekoľkých intervalov alebo funkcia na rôznych intervaloch je daná rôznymi vzorcami, potom na nájdenie oblasti hodnôt funkcie je potrebné nájsť množiny hodnôt funkcie na každom intervale a zoberte ich spojenie.
Príklad 7: Nájdite rozsahy f(x) A f(f(x)), Kde
f(x) na lúči (-∞;1], kde sa zhoduje s výrazom 4 x + 9 4 -x + 3. Označme t = 4 x. Potom f(x) = t + 9/t + 3, kde 0< t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x) na lúči (-∞;1] sa zhoduje s množinou hodnôt funkcie g(t) = t + 9/t + 3, na intervale (0;4], ktorý nájdeme pomocou derivácie g'(t) = 1 – 9/t2. Na intervale (0;4] derivácia g'(t) je definovaný a zaniká tam pri t = 3. O 0<t<3 она отрицательна, а при 3<t<4 положительна. Следовательно, в интервале (0;3) функция g(t) klesá a v intervale (3;4) sa zvyšuje, pričom zostáva súvislý počas celého intervalu (0;4), takže g (3)= 9 – najmenšia hodnota tejto funkcie na intervale (0;4], pričom jej najväčšia hodnota neexistuje, takže keď t→0 funkcia vpravo g(t)→+∞. Potom vlastnosťou spojitej funkcie množina hodnôt funkcie g(t) na intervale (0;4], a teda súbor hodnôt f(x) na (-∞;-1], bude lúč .
Teraz skombinujte intervaly - množiny funkčných hodnôt f(f(x)), označovať t = f(x). Potom f(f(x)) = f(t), kde Pre zadané t funkciu f(t)= 2 cos( x-1) 1/2+ 7 a opäť nadobúda všetky hodnoty od 5 do 9 vrátane, t.j. rozsah E(fІ) = E(f(f(x))) =.
Podobne označovanie z = f(f(x)), môžete nájsť rozsah hodnôt E(f 3) funkcie f(f(f(x))) = f(z), kde 5 ≤ z ≤ 9 atď. Uistite sa, že E(f3) = .
Najuniverzálnejšia metóda hľadania množiny funkčných hodnôt je použitie najväčších a najmenších hodnôt funkcie v danom intervale.
Príklad 8. Pri akých hodnotách parametrov R nerovnosť 8 x - р ≠ 2 x+1 – 2 x platí pre všetky -1 ≤ x< 2.
Po určení t = 2x, zapíšeme nerovnosť do tvaru р ≠ t 3 – 2t 2 + t. Pretože t = 2x– funkcia nepretržitého zvyšovania zapnutá R, potom pre -1 ≤ x< 2 переменная
2 -1 ≤ t<2 2 ↔
0,5 ≤ t< 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда R odlišné od funkčných hodnôt f(t) = t3 – 2t2 + t pri 0,5 ≤ t< 4.
Najprv nájdime množinu hodnôt funkcie f(t) v segmente, kde má všade derivát f’(t) = 3t2 – 4t + 1. teda f(t) je diferencovateľný, a teda spojitý na intervale. Z rov. f'(t) = 0 nájsť kritické body funkcie t = 1/3, t = 1, z ktorých prvý nepatrí do segmentu a druhý do neho patrí. Pretože f(0,5) = 1/8, f(1) = 0, f(4) = 36, potom podľa vlastnosti diferencovateľnej funkcie je 0 najmenšia a 36 je najväčšia hodnota funkcie f(t) na segmente. Potom f(t), ako spojitá funkcia nadobúda v intervale všetky hodnoty od 0 do 36 vrátane a hodnotu 36 nadobúda len vtedy, t = 4, teda pre 0,5 ≤ t< 4, она принимает все значения из промежутка и f(X) - funkcia
a) kvadratický,
b) logaritmické,
c) demonštratívne;
2) E(f(X)) = R \{7}.
Pri diskusii o úlohe 2samostatnej práce upozorniť žiakov na to, že v prípade monotónnosti a nadväznosti funkcie y=f(X)v danom intervale[a;b],jeho mnoho významov-interval,ktorých konce sú hodnoty f(a)a f(b).
Možnosti odpovede pre úlohu 3.
1.
A) r = –X 2 + 2 , r = –(X
+ 18) 2 + 2,
r= a(X – X c) 2 + 2 at A < 0.
b) r= –| denník 8 X | + 2,
V) r = –| 3 X – 7 | + 2, r = –5 | X | + 3.
2.
a) b)
V) r = 12 – 5X, Kde X ≠ 1 .
Nájdenie viacerých hodnôt funkcie pomocou derivácie
učiteľ. V 10. ročníku sme sa oboznámili s algoritmom hľadania extrémov spojitej funkcie na segmente a hľadania jej množiny hodnôt bez spoliehania sa na graf funkcie. Pamätáte si, ako sme to urobili? ( Použitie derivátu.) Zapamätajme si tento algoritmus .
1. Skontrolujte funkciu r = f(X) je definovaný a súvislý na segmente J = [a; b]. 2. Nájdite hodnoty funkcie na koncoch segmentu: f(a) a f(b). Komentujte. Ak vieme, že funkcia je spojitá a monotónna J, potom môžete okamžite odpovedať: E(f) = [f(a); f(b)] alebo E(f) = [f(b); f(A)]. 3. Nájdite deriváciu a potom kritické body x kJ. 4. Nájdite hodnoty funkcie v kritických bodoch f(x k). 5. Porovnajte funkčné hodnoty f(a), f(b) A f(x k), vyberte najväčšiu a najmenšiu hodnotu funkcie a uveďte odpoveď: E(f)= [f názov; f naíb]. |
Problémy s použitím tohto algoritmu sa vyskytujú vo verziách jednotnej štátnej skúšky. Napríklad v roku 2008 bola takáto úloha navrhnutá. Musíte to vyriešiť Domy .
Úloha C1. Nájdite najväčšiu hodnotu funkcie
f(X) = (0,5X + 1) 4 – 50(0,5X + 1) 2
v | X + 1| ≤ 3.
Podmienky domácej úlohy sú vytlačené pre každého študenta .
Nájdenie množiny hodnôt komplexnej funkcie
učiteľ. Hlavnou časťou našej lekcie budú neštandardné úlohy obsahujúce zložité funkcie, ktorých deriváty sú veľmi zložité výrazy. A grafy týchto funkcií sú nám neznáme. Preto na riešenie použijeme definíciu komplexnej funkcie, teda závislosť medzi premennými v poradí ich vnorenia do danej funkcie, a odhad ich rozsahu hodnôt (interval zmeny ich hodnoty). Problémy tohto typu sa nachádzajú v druhej časti jednotnej štátnej skúšky. Pozrime sa na niekoľko príkladov.
Cvičenie 1. Pre funkcie r = f(X) A r = g(X) napíšte komplexnú funkciu r = f(g(X)) a nájdite jeho množinu hodnôt:
A) f(X) = –X 2 + 2X +
3, g(X) = hriech X;
b) f(X) = –X 2 + 2X +
3, g(X) = log 7 X;
V)
g(X) = X 2 + 1;
G)
Riešenie. a) Komplexná funkcia má tvar: r= – hriech 2 X+ 2 hriechy X + 3.
Uvádzame prechodný argument t, môžeme túto funkciu napísať takto:
r= –t 2 + 2t+ 3, kde t= hriech X.
Pri internej funkcii t= hriech X argument má ľubovoľné hodnoty a množinou jeho hodnôt je segment [–1; 1].
Teda pre vonkajšiu funkciu r = –t 2 +2t+ 3 sme zistili interval na zmenu hodnôt jeho argumentu t: t[-1; 1]. Pozrime sa na graf funkcie r = –t 2 +2t + 3.
Poznamenávame, že kvadratická funkcia pri t[-1; 1] má na koncoch najmenšie a najväčšie hodnoty: r meno = r(–1) = 0 a r naib = r(1) = 4. A keďže táto funkcia je spojitá na intervale [–1; 1], potom akceptuje všetky hodnoty medzi nimi.
Odpoveď: r .
b) Zloženie týchto funkcií nás vedie ku komplexnej funkcii, ktorú po zavedení medziargumentu možno znázorniť takto:
r= –t 2 + 2t+ 3, kde t= denník 7 X,
Funkcia t= denník 7 X
X (0; +∞ ), t (–∞ ; +∞ ).
Funkcia r = –t 2 + 2t+ 3 (pozri graf) argument t má akékoľvek hodnoty a samotná kvadratická funkcia má všetky hodnoty nie viac ako 4.
Odpoveď: r (–∞ ; 4].
c) Komplexná funkcia má nasledujúci tvar:
Zavedením prechodného argumentu dostaneme:
Kde t = X 2 + 1.
Keďže pre vnútornú funkciu X R , A t .
Odpoveď: r (0; 3].
d) Zloženie týchto dvoch funkcií nám dáva komplexnú funkciu
ktoré možno napísať ako
Všimni si
Takže keď
Kde k Z , t [–1; 0) (0; 1].
Nakreslením grafu funkcie vidíme to pri týchto hodnotách t
r(–∞ ; –4] c ;
b) v celej oblasti definície.
Riešenie. Najprv preskúmame monotónnosť tejto funkcie. Funkcia t= arcctg X- nepretržitý a klesajúci o R a množina jeho hodnôt (0; π). Funkcia r= log 5 t je definovaný na intervale (0; π), je spojitý a na ňom rastie. To znamená, že táto komplexná funkcia sa na súprave znižuje R . A ako zloženie dvoch spojitých funkcií bude spojité ďalej R .
Poďme vyriešiť problém "a".
Keďže funkcia je spojitá na celej číselnej osi, je spojitá na ktorejkoľvek jej časti, najmä na danom segmente. A potom v tomto segmente má najmenšie a najväčšie hodnoty a preberá všetky hodnoty medzi nimi:
f(4) = log 5 arcctg 4.
Ktorá z výsledných hodnôt je väčšia? prečo? A aký bude súbor hodnôt?
odpoveď: 
Poďme vyriešiť problém "b".
odpoveď: pri(–∞ ; log 5 π) v celej oblasti definície.
Problém s parametrom
Teraz skúsme vytvoriť a vyriešiť jednoduchú rovnicu s parametrom tvaru f(X) = a, Kde f(X) - rovnaká funkcia ako v úlohe 4.
Úloha 5. Určte počet koreňov rovnice log 5 (arcctg X) = A pre každú hodnotu parametra A.
Riešenie. Ako sme už ukázali v úlohe 4, funkcia pri= log 5 (arcctg X) - klesá a stále svieti R a nadobúda hodnoty menšie ako log 5 π. Tieto informácie stačia na odpoveď.
odpoveď: Ak A < log 5 π, то уравнение имеет единственный корень;
Ak A≥ log 5 π, potom neexistujú žiadne korene.
učiteľ. Dnes sme sa pozreli na problémy súvisiace s hľadaním množiny hodnôt funkcie. Na tejto ceste sme objavili novú metódu riešenia rovníc a nerovníc - metódu odhadu, takže nájdenie množiny funkčných hodnôt sa stalo prostriedkom na riešenie problémov vyššej úrovne. Pritom sme videli, ako sa takéto problémy konštruujú a ako vlastnosti monotónnosti funkcie uľahčujú ich riešenie.
A rád by som dúfal, že logika, ktorá spájala dnes diskutované úlohy, vás ohromila alebo aspoň prekvapila. Nemôže to byť inak: výstup na nový vrchol nenechá nikoho ľahostajným! Všímame si a oceňujeme krásne obrazy, sochy atď. Ale aj matematika má svoju krásu, príťažlivú a očarujúcu – krásu logiky. Matematici hovoria, že krásne riešenie je zvyčajne správne riešenie, a to nie je len fráza. Takéto riešenia si teraz musíte nájsť sami a jednu z ciest k nim sme dnes naznačili. Veľa šťastia! A pamätajte: ten, kto kráča, ovláda cestu!
Funkcia je jedným z najdôležitejších matematických pojmov.
Definícia: Ak je každé číslo z určitej množiny x spojené s jedným číslom y, potom hovoria, že na tejto množine je definovaná funkcia y(x). V tomto prípade sa x nazýva nezávislá premenná alebo argument a y sa nazýva závislá premenná alebo hodnota funkcie alebo jednoducho funkcia.
Premenná y je tiež funkciou premennej x.
Po označení zhody písmenom, napríklad f, je vhodné napísať: y=f (x), čiže hodnotu y získame z argumentu x pomocou zhody f. (Prečítajte si: y sa rovná f z x.) Symbol f (x) označuje hodnotu funkcie zodpovedajúcu hodnote argumentu rovnajúcej sa x.
Príklad 1 Nech je funkcia daná vzorcom y=2x 2 –6. Potom môžeme napísať, že f(x)=2x 2 –6. Nájdite hodnoty funkcie pre hodnoty x rovné napríklad 1; 2,5;–3; t.j. nájdeme f(1), f(2,5), f(–3):
f(1)=212 –6=–4;
f(2,5)=2 2,52-6=6,5;
f(–3)=2 (–3) 2 –6= 12.
Všimnite si, že v zápise tvaru y=f (x) sa namiesto f používajú iné písmená: g atď.
Definícia: Doména funkcie sú všetky hodnoty x, pre ktoré funkcia existuje.
Ak je funkcia špecifikovaná vzorcom a jej doména definície nie je špecifikovaná, potom sa doména definície funkcie považuje za pozostávajúcu zo všetkých hodnôt argumentu, pre ktoré má vzorec zmysel.
Inými slovami, doménou funkcie danej vzorcom sú všetky hodnoty argumentu okrem tých, ktorých výsledkom sú akcie, ktoré nemôžeme vykonať. V súčasnosti poznáme len dve takéto akcie. Nemôžeme deliť nulou a nemôžeme brať druhú odmocninu zo záporného čísla.
Definícia: Všetky hodnoty, ktoré závislá premenná tvorí rozsah funkcie.
Oblasť definície funkcie popisujúcej reálny proces závisí od konkrétnych podmienok jej výskytu. Napríklad závislosť dĺžky l železnej tyče od teploty ohrevu t je vyjadrená vzorcom, kde l 0 je počiatočná dĺžka tyče a je lineárny koeficient rozťažnosti. Tento vzorec má zmysel pre akékoľvek hodnoty t. Definičný obor funkcie l=g(t) je však interval niekoľkých desiatok stupňov, pre ktorý platí zákon lineárnej expanzie.
Príklad.
Zadajte rozsah funkcií y = arcsinx.
Riešenie.
Definičnou doménou arcsínusu je segment [-1; 1]
. Nájdite najväčšiu a najmenšiu hodnotu funkcie na tomto segmente.
Derivát je pozitívny pre každého X z intervalu (-1; 1)
, to znamená, že funkcia arcsínus sa zvyšuje v celej oblasti definície. Preto má najmenšiu hodnotu kedy x = -1, a najväčší na x = 1.
Získali sme rozsah funkcie arcsínus 
.
Nájdite množinu funkčných hodnôt 
na segmente
.
Riešenie.
Nájdite najväčšiu a najmenšiu hodnotu funkcie na danom segmente.
Určme extrémne body patriace segmentu
: